our cat
Hayato Itoh
PhD Eng.
Assistant Professor
Department of Applied Mathematics, Faculty of Science, Fukuoka University
E-mail: hitoh [a t] fukuoka-u.ac.jp
Visiting Scholar
Department of Intelligent Systems, Graduate School of Informatics, Nagoya University
E-mail: hitoh [a t] mori.m.is.nagoya-u.ac.jp

I am a researcher at Fukuoka University. I completed my PhD at Chiba University under the supervision of Prof. Atsushi Imiya. After I got my PhD, I moved to Mori Lab. at Nagoya University. As a postdoc (research fellow) for AMED projects [a, b], I contributed to developing computer-aided-diagnosis systems, which are released as EndoBrain (Japanese/English), EndBrain-Eye (Japanese/English), and EndoBrain-Plus (Japanese) for colonoscopy.

My research is in pattern recognition. I am particularly interested in mathematical and geometrical aspects of feature representations.
Recent Activities
Research Topics

Tensorial Pattern Recognition

MappingConditions
Dimension reduction and construction of feature space
We mathematically and experimentally evaluated the validity of dimension-reduction methods for the computation of similarity in image pattern recognition. Image pattern recognition identifies instances of particular objects and distinguishes differences among images. This recognition uses pattern recognition techniques for the classification and categorisation of images. In numerical image pattern recognition techniques, images are sampled using an array of pixels. This sampling procedure derives vectors in a higher-dimensional metric space from image patterns. To ensure the accuracy of pattern recognition techniques, the dimension reduction of the vectors is an essential methodology since the time and space complexities of processing depend on the dimension of the data. Dimension reduction causes information loss of topological and geometrical features of image patterns. Through both theoretical and experimental comparisons, we clarified that dimension-reduction methodologies that preserve the topology and geometry in the image pattern space are essential for linear pattern recognition.

• Hayato Itoh, Atsushi Imiya, Tomoya Sakai, Dimension reduction and construction of feature space for image pattern recognition, Journal of Mathematical Imaging and Vision, vol. 56, issule 1, pp. 1-31, 2016. DOI: 10.1007/s10851-015-0629-1, SharedIt
• Hayato Itoh, Tomoya Sakai, Kazuhiko Kawamoto, Atsushi Imiya: Dimension reduction methods for image pattern recognition, In Proc. Second International Workshop, on Similarity-Based Pattern Analysis and Recognition, Lecture Notes in Computer Science, vol. 7953 pp. 26-42, 2 2013
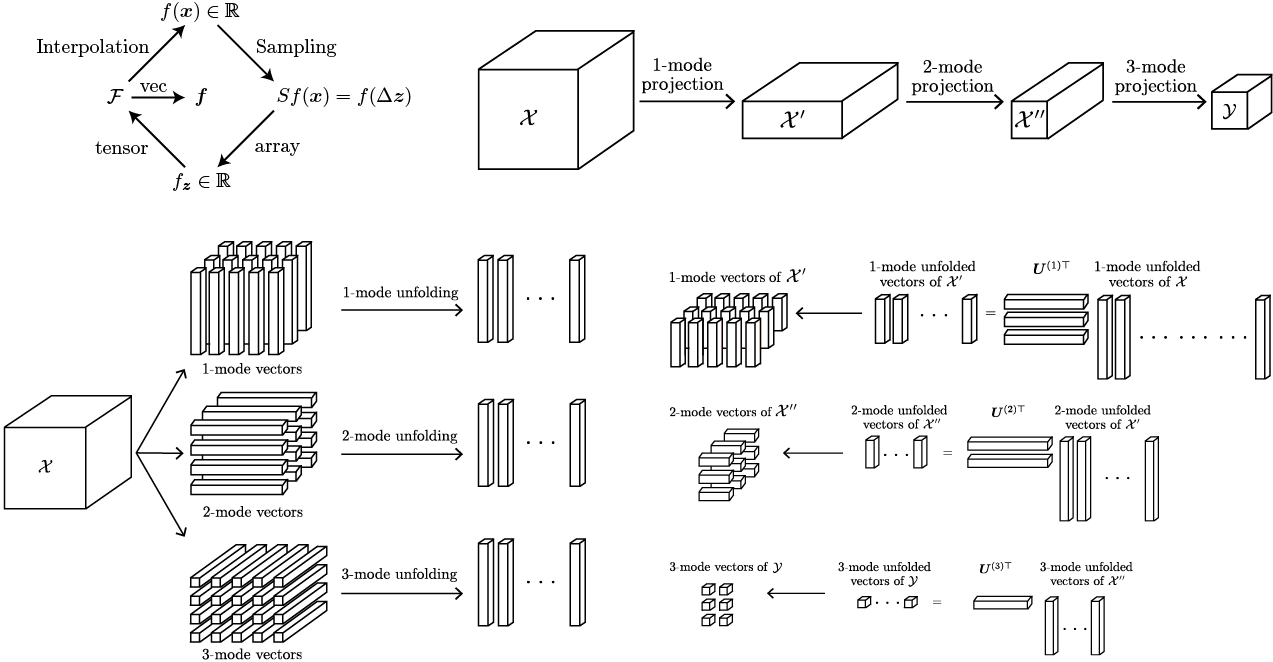
TensorExpression
Pattern recognition of tensorial data in multilinear space
We defined tensor subspace method for pattern recognition. This method is the natural extension of subspace method. For numerical computation, we deal with sampled patterns. In traditional pattern recognition, these sampled patterns are embedded in an appropriate-dimensional Euclidean space as vectors. The other way is to deal with sampled patterns as higher-dimensional array data. Tensors allow expressing multidimensional array data in multilinear forms. We expressed these array data by tensors to preserve multilinearity of function in the original pattern space. A tensor projection expresses a multilinear subspace of a category and derives a similarity of a query to a category.

• Hayato Itoh, Atsushi Imiya, Tomoya Sakai, Pattern recognition in multilinear space and its applications: mathematics, computational algorithms and numerical validations, Machin Vision and Applications, vol. 27, pp. 1259–1273, 2016. DOI: 10.1007/s00138-016-0806-2, SharedIt
• Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Mathematical Aspects of Tensor Subspace Method. In Proc. S+SSPR, Lecture Notes in Computer Science , vol. 10029, pp. 37-48, 2016
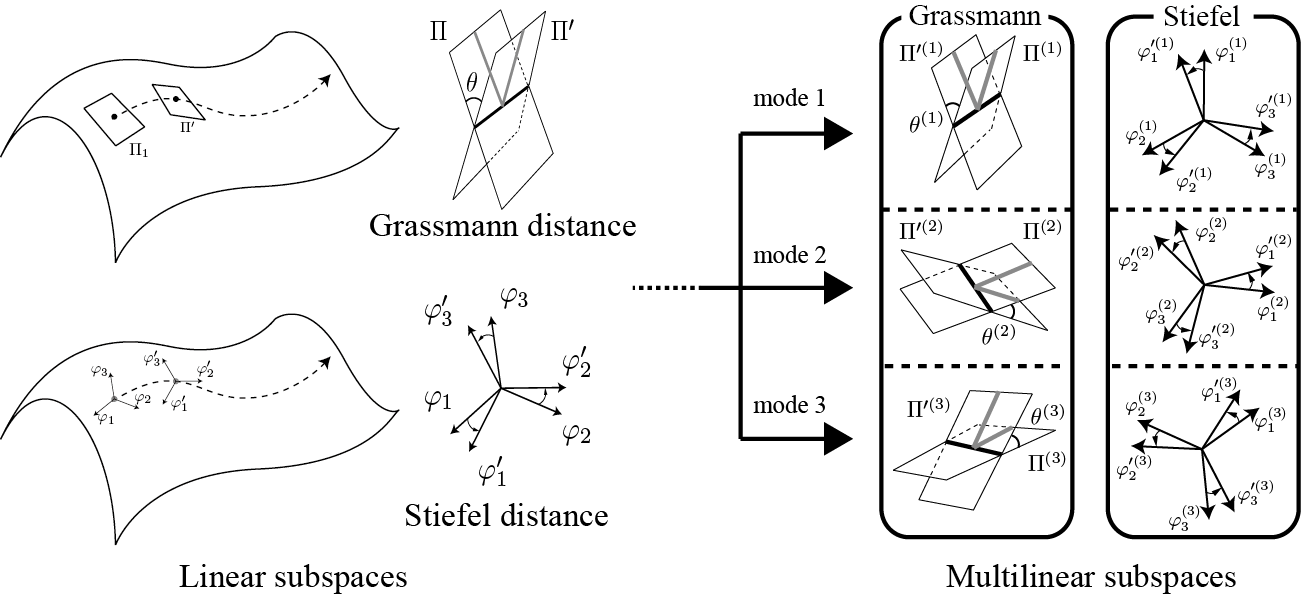
GeodesicDistancee
Geodesic distance between multilinear subspaces
We defined geodesic distances between multilinear subspaces for pattern recognition. Sampled values of volumetric data are expressed as three-way array data, which is expressed as tensors. Multi-way forms of volumetric data require quantitative methods for the discrimination of multi-way forms. Therefore, we define geodesic measures for multilinear subspaces of multi-way data arrays using transportation between the Stiefel manifolds.

• Hayato Itoh, Atsushi Imiya: Subspace Discrimination for Multiway Data, Journal of Mathematical Imaging and Vision, vol. 66, pp. 657–677 (August, 2024), DOI: 10.1007/s10851-024-01188-9, SharedIt, 2024
• Hayato Itoh, Atsushi Imiya: Multilinear Subspace Method Based on Geodesic Distance for Volumetric Object Classification, In Proc. International Conference on Computer Analysis of Images and Patterns, LNCS vol. 11678, pp. 672-683, 2019
• Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Distances Between Tensor Subspaces, In Applications of Intelligent Systems, Frontiers in Artificial Intelligence and Applications, vol. 310, pp. 50-59, 2018
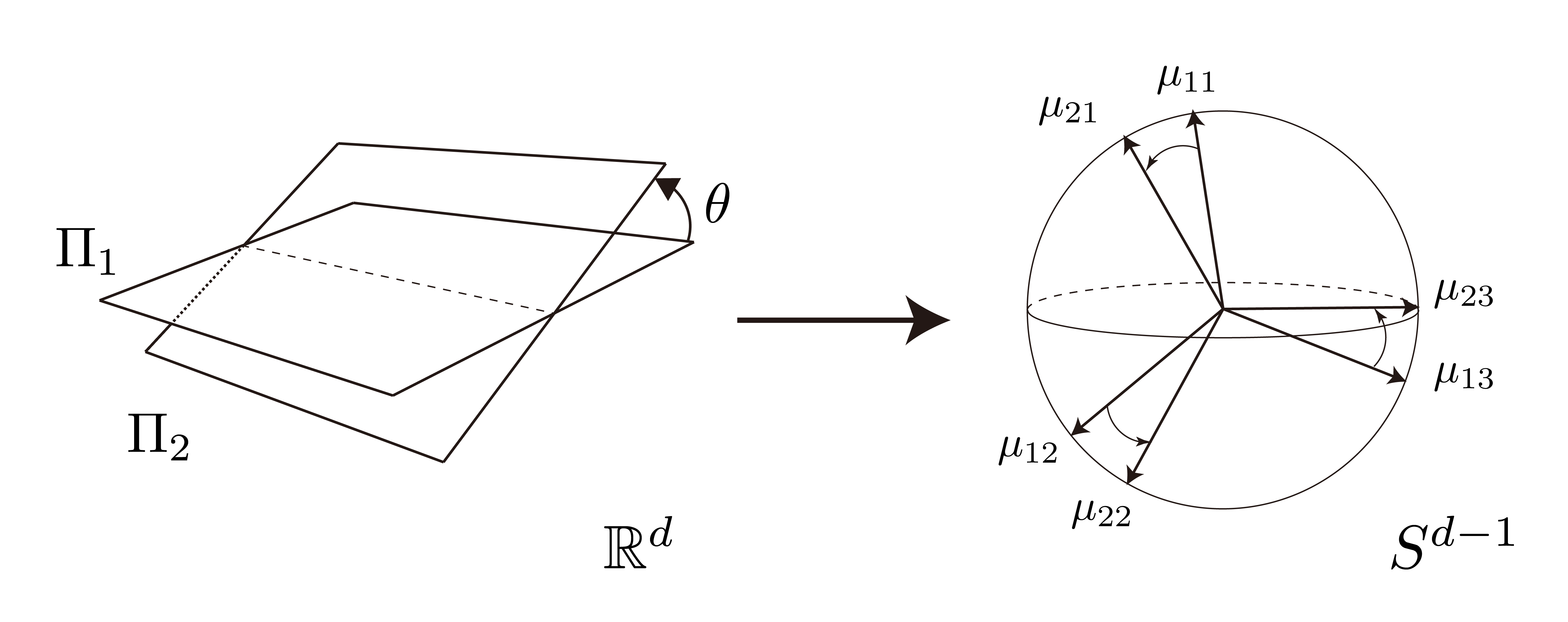
GeodesicDistancee
Subspace method on a unit shpere
Principal component analysis usually finds a small number of principal components to analyse and represent a set of sampled patterns. In traditional pattern recognition and machine learning, many works use subspaces given by PCA, that is, by eigendecomposition of the data covariance matrix or singular value decomposition of the data matrix, to represent categories. These works define pattern classifiers by using a canonical angle between two subspaces. However, many of them focus on only eigenvectors for spanning a subspace and discard a distribution of eigenvalues, even though eigenvalues express the variances of patterns along each eigenvector. We integrated the distributions of eigenvalues on eigenvectors as probability measures on the Stiefel manifold of k = 1. For subspace discrimination, we introduced the transport distance between two probability measures on a unit sphere.

• Hayato Itoh, Atsushi Imiya: Subspace Discrimination for Multiway Data, Journal of Mathematical Imaging and Vision, vol. 66, pp. 657–677 (August, 2024), DOI: 10.1007/s10851-024-01188-9, SharedIt, 2024

Medical Image Understanding

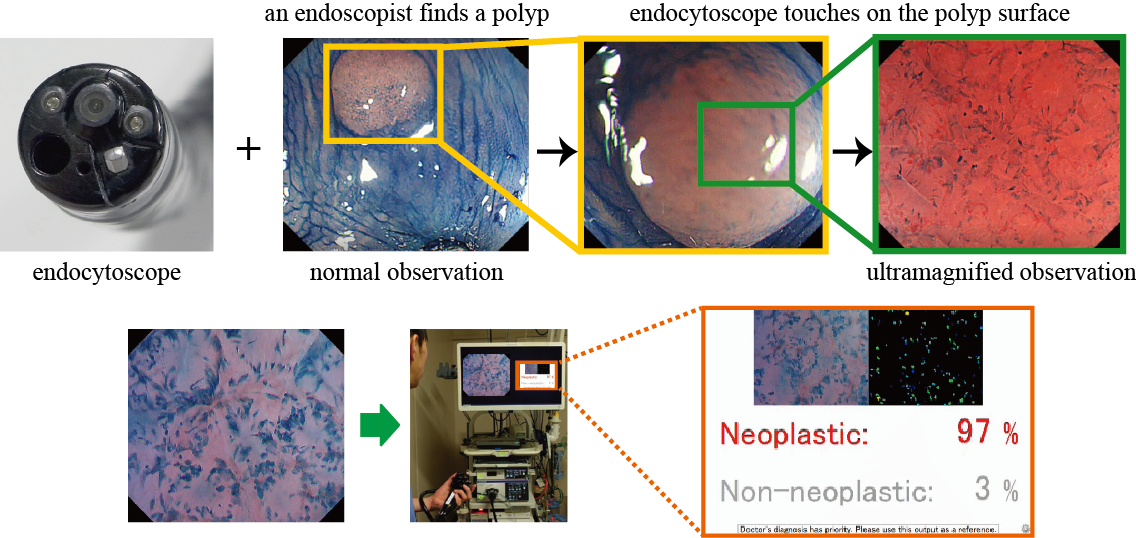
ECClassificaiton
Neoplasia recognition by endocytoscopic images
An endocytoscope is a new type of endoscope that enables users to perform conventional endoscopic observation and ultramagnified observation at the cell level. Based on this ultramagnified observation, endoscopists can classify a polyp into non-neoplastic and neoplastic (adenoma and invasive cancer) lesions. This endocytoscopy is expected to improve the cost-effectiveness of colonoscopy. However, endocytoscopy requires much knowledge and high-level experience. For the support of novices in the endocytoscopy, analysis and automated classification techniques of endocytoscopic images have potential demands. In this topic, we developed a feature-extraction method for the endocytoscopic images and used it for automated endocytoscopic-image classification. We analysed the differences of distributions of extracted features among several institutions. Futhermore, we evaluated the generalisation ability of our classification method.

• Hayato Itoh, et al., Robust endocytoscopic image classification based on higher-order symmetric tensor analysis and multi-scale topological statistics, International Journal of Computer Assisted Radiology and Surgery vol. 15, pp. 2049–2059, 2020. DOI: 10.1007/s11548-020-02255-3, SharedIt
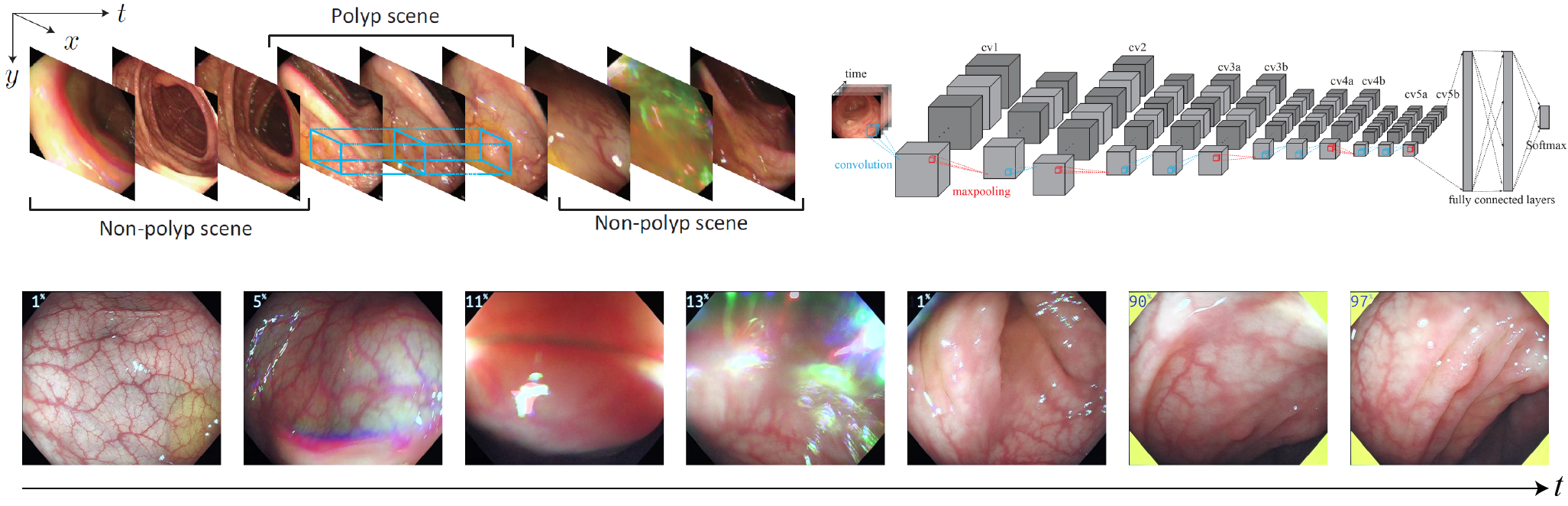
PolypDetection
Polyp detection from colonoscopic videos
Automated polyp detection is a vital technique for the analysis of colonoscopic images and videos. Furthermore, the detection technique has potential demands for the support of colonoscopists in their diagnosis. For example, this technique prevents colonoscopists' overlooking of polyps, and every 1% increase in the polyp-detection rate can decrease the interval of colorectal cancer incidence by 3%. We proposed a detection method and constructed a publicly-available evaluation dataset: SUN colonoscopy video database

• Hayato Itoh, et al., Stable polyp-scene classification via subsampling and residual learning from an imbalanced large dataset, IET Healthcare Technology Letters, vol. 6, issue 6, pp. 237-242, 2019. DOI: 10.1049/htl.2019.0079
DepthEstimation
Depth estimation from a single colonoscopic image
A three-dimensional structure extraction of a colon-wall shape is an essential task for colonoscopic image understanding. For example, polyp-size estimation requires 3D information of a polyp's shape. Using domain translations with a Lambertian-reflection model, we developed a depth estimation method and evaluated its accuracy for colonoscopy (Left: input, Middle: generated virtual image, Right: estimated detph).

• Hayato Itoh, et al., Unsupervised colonoscopic depth estimation by domain translations with a Lambertian-reflection keeping auxiliary task, International Journal of Computer Assisted Radiology and Surgery, vol. 16, pp. 989–1001, 2021. DOI: 10.1007/s11548-021-02398-x, SharedIt
PolypSizeClassificaiton
Polyp-size classification from colonoscopic images
Polyp-size estimation is vital for colonoscopy. However, endoscopists' subjective estimations accompany the terminal digit bias and result in uncertain polyp-size determination. We developed a binary polyp-size classification method by integrating polyp localisaiton into depth estimation. The extracted depth around a polyp expresses 3D information of a polyp shape, which contributes to automated polyp-size estimation.

• Hayato Itoh, et al., Towards automated colonoscopy diagnosis: binary polyp size estimation via unsupervised depth learning, In Proc. MICCAI2018, LNCS, vol. 11071, pp. 611-619, 2018
• Hayato Itoh, et al., Binary polyp-size classification based on deep-learned spatial information, International Journal of Computer Assisted Radiology and Surgery, vol. 16, pp. 1817–1828, 2021. DOI: 10.1007/s11548-021-02477-z, SharedIt
PolypLocalisation
Analysis of a deep-learning model in polyp detection
Precise polyp detection and localisation are essential for colonoscopy diagnosis. Statistical machine learning with a large-scale dataset achieved accurate bounding-box-based polyp detection and contributed to the construction of CAD systems. However, precise automated polyp localisation is still challenging. We proposed new visual explaining methods for a well-trained object detector towards a precise automated polyp localisation (Left: polyp detection, Middle: object activation mapping, Right: Shape activation mapping, the target polyp is a flat type (IIa)).

• Hayato Itoh, et al., Positive-Gradient Weighted Object Activation Mapping: Visual Explanation of Object Detector Towards Precise Colorectal-Polyp Localisation, International Journal of Computer Assisted Radiology and Surgery, vol. 17, issue 11, pp. 2051-2063, 2022. DOI: 10.1007/s11548-022-02696-y, SharedIt
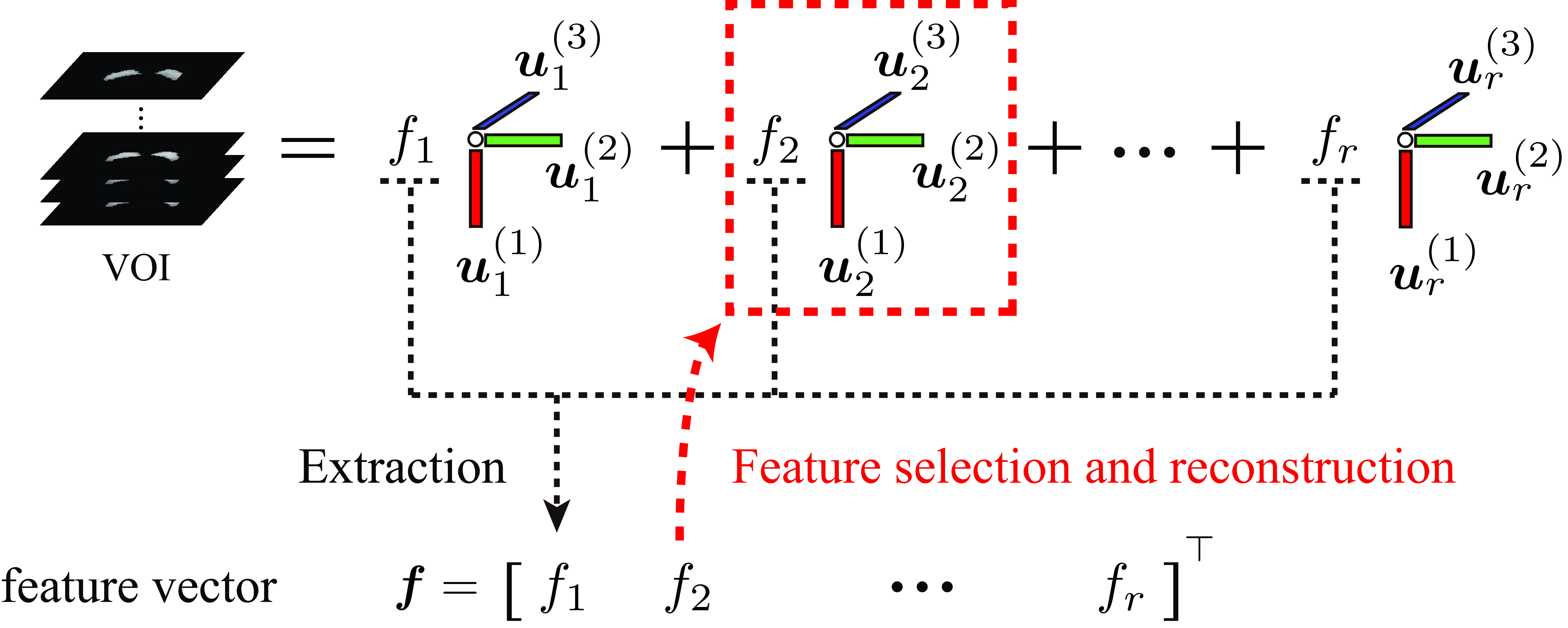
PolypLocalisation
Tensorial expression of MRI data for feature extraction, selection and visualisation
Exploring disease-related three-dimensional patterns in captured volumetric human-body data is essential for medical image understanding and image-based diagnosis. We analysed the Parkinson's disease-related three-dimensional patterns by decomposing neuromelanin-sensitive MRI data as third-, fourth- and fifth-order tensors. Visualised three-dimensional patterns via our discriminative feature selection show the importance of the intensity changes in the ventrolateral tiers of the substantia nigra.

• Hayato Itoh, et al., Preliminary Study of Substantia Nigra Analysis by Tensorial Feature Extraction, International Journal of Computer Assisted Radiology and Surgery, DOI: 10.1007/s11548-024-03175-2, SharedIt
• Hayato Itoh, et al., Pattern Analysis of Substantia Nigra in Parkinson Disease by Fifth-Order Tensor Decomposition and Multi-sequence MRI, Proc. 3rd International Workshop on Multiscale Multimodal Medical Imaging (MMMI 2022) in conjunction with 25th MICCAI2022, LNCS vol. 13594, pp. 63–75, 2022.
Publications

Open Dataset

  1. SUN Colonoscopy Video Database: a dataset for the evaluation of an automated colorectal-polyp detection. This dataset consists of 158,690 colonoscopic images including 100 polyps with bounding-box annotations.

Journal Paper

  1. Hayato Itoh, Masahiro Oda, Shinji Saiki, Koji Kamagata, Wataru Sako, Kei-ichi Ishikawa, Nobutaka Hattori, Shigeki Aoki, Kensaku Mori: Preliminary Study of Substantia Nigra Analysis by Tensorial Feature Extraction, International Journal of Computer Assisted Radiology and Surgery, vol. 19, pp. 2133-2142 (November 2024)(27 June 2024, online first), DOI: 10.1007/s11548-024-03175-2, SharedIt, IF: 3.1
  2. Hayato Itoh, Atsushi Imiya: Subspace Discrimination for Multiway Data, Journal of Mathematical Imaging and Vision, vol. 66, pp. 657–677 (August, 2024) (25th May 2024, online first), DOI: 10.1007/s10851-024-01188-9, SharedIt, IF: 1.6
  3. Cesare Hassan, Masashi Misawa, Tommy Rizkala, Yuichi Mor, Shahnaz Sultan, Antonio Facciorusso, Giulio Antonelli, Marco Spadaccini, Britt B.S.L. Houwen, Emanuele Rondonotti, Harsh Patel, Kareem Khalaf, James Weiquan Li, Gloria M. Fernandez, Pradeep Bhandari, Evelien Dekker, Seth Gross, Tyler Berzin, Per Olav Vandvik, Loredana Correale, Shin-ei Kudo, Prateek Sharma, Douglas K. Rex, Alessandro Repici, Farid Foroutan, CADx Analysis Study Group (Roberta Maselli, Silvia Carrara, Alessandro Fugazza, Antonio Capogreco, Maddalena Menini, Davide Massimi, Kazumi Takishima, Kenichi Mochizuki, Yuki Miyata, Kentaro Mochida, Yoshika Akimoto, Takanori Kuroki, Yuriko Morita, Osamu Shiina, Shun Kato, Ishita Barua, Øyvind Holme, Paulina Wieszczy, Magnus Løberg, Mette Kalager, Shraddha Gulati, Sophie Williams, Bu Hayee, Mehul Patel, Nishmi Gunasingam, Alexandra Kent, Andrew Emmanuel, Amyn Haji, Hayato Itoh, Kensaku Mori, Tetsuo Nemoto, Carl Munck, Jens Aksel Nilsen, Stine Astrup Hvattum, Svein Oskar Frigstad, Petter Tandberg, Davide Lanza, Giacomo Bonanno): Computer-Aided Diagnosis for Leaving Colorectal Polyps In Situ : A Systematic Review and Meta-analysis, Computer-Aided Diagnosis for Leaving Colorectal Polyps In Situ : A Systematic Review and Meta-analysis, Annals of Internal Medicine, vol. 177, no. 7, pp. 919-928 (July, 2024) (21st May, 2024, online first), DOI: 10.7326/M23-2865, IF: 39.2
  4. Kento Hosoya, Kouki Nozawa, Hayato Itoh, Atsushi Imiya: Mathematical Properties of Pyramid-Transform-Based Resolution Conversion and Its Applications, Journal of Mathematical Imaging and Vision, vol. 66, pp. 115–153 (March, 2024) (25th Dec, 2023 online first), DOI: 10.1007/s10851-023-01166-7, IF: 2.0
  5. Cheng Wang, Masahiro Oda, Yuichiro Hayashi, Takayuki Kitasaka, Hayato Itoh, Hirotoshi Honma, Hirotsugu Takabatake, Masaki Mori, Hiroshi Natori, Kensaku Mori: Anatomy Aware-based 2.5D Bronchoscope Tracking for Image-guided Bronchoscopic Navigation, Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, vol. 11, no. 4, pp. 1122-1129 (July, 2023) DOI: 10.1080/21681163.2022.2152728, IF: 1.6
  6. Kinichi Hotta, Hayato Itoh, Yuichi Mori, Masashi Misawa, Kensaku Mori, Shin-ei Kudo: Computer-Aided Size Estimation of Colorectal Polyps, Techniques and Innovations in Gastrointestinal Endoscopy, vol. 25, issue 2, pp. 186-188 (April 2023) DOI: 10.1016/j.tige.2022.11.004, IF: 2.4
  7. Kai Jiang, Hayato Itoh, Msahiro Oda, Taishi Okumura, Yuichi Mori, Masashi Misawa, Takemasa Hayashi, Shin-Ei. Kudo, Kensaku Mori: Gaussian Affinity and GIoU-based Loss for Perforation Detection and Localization from Colonoscopy Videos, International Journal of Computer Assisted Radiology and Surgery, vol. 18, issue 5, pp. 795-805 (March 2023) DOI: 10.1007/s11548-022-02821-x, IF: 3.0
  8. Hayato Itoh, Masashi Misawa, Yuichi Mori, Shin-Ei Kudo, Masahiro Oda, Kensaku Mori: Positive-Gradient Weighted Object Activation Mapping: Visual Explanation of Object Detector Towards Precise Colorectal-Polyp Localisation, International Journal of Computer Assisted Radiology and Surgery, vol. 17, issue 11, pp. 2051-2063 (November 2022) DOI: 10.1007/s11548-022-02696-y, Nagoya Repository, SharedIt, IF: 3.4.
  9. Hayato Itoh, Masahiro Oda, Kai Jiang, Yuichi Mori, Masashi Misawa, Shin-Ei Kudo, Kenichiro Imai, Sayo Ito, Kinichi Hotta, Kensaku Mori: Uncertainty Meets 3D-Spatial Feature in Colonoscopic Polyp-Size Determination, Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, vol. 10, Issue 3, pp. 289-298 (May 2022) DOI: 10.1080/21681163.2021.2004445, IF:1.6
  10. Masahiro Oda, Hayato Itoh, Kiyohito Tanaka, Hirotsugu Takabatake, Masaki Mori, Hiroshi Natori, Kensaku Mori: Depth Estimation from Single-shot Monocular Endoscope Image Using Image Domain Adaptation And Edge-Aware Depth Estimation, Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, vol. 10, issue 3, pp. 266-273 (May 2022) DOI: 10.1080/21681163.2021.2012835, IF: 1.6
  11. Diba Ainechi, Masashi Misawa, Ishita Barua, Solveig Linnea Veen Larsen,Vemund Paulsen, Kjetil Kjeldstad Garborg, Lars Aabakken, Christer Julseth Tønnesen, Magnus Løberg, Mette Kalager, Shin-Ei Kudo, Kinichi Hotta, Kazuo Ohtsuka, Shoichi Saito, Hiroaki Ikematsu, Yutaka Saito, Takahisa Matsuda, Hayato Itoh, Kensaku Mori, Michael Bretthauer, Yuichi Mori: Impact of artificial intelligence on colorectal polyp detection for early-career endoscopists: an international comparative study, Scandinavian Journal of Gastroenterology, vol. 57, pp. 1272-1277 (May 2022) DOI: 10.1080/00365521.2022.2070436, IF: 3.0
  12. Ishita Barua, Paulina Wieszczy, Shin-ei Kudo, Masashi Misawa, Øyvind Holme, Shraddha Gulati, Sophie Williams, Kensaku Mori, Hayato Itoh, Kazumi Takishima, Kenichi Mochizuki, Yuki Miyata, Kentaro Mochida, Yoshika Akimoto, Takanori Kuroki, Yuriko Morita, Osamu Shiina, Shun Kato, Tetsuo Nemoto, Bu Hayee, Mehul Patel, Nishmi Gunasingam, Alexandra Kent, Andrew Emmanuel, Carl Munck, Jens Aksel Nilsen, Stine Astrup Hvattum, Svein Oskar Frigstad, Petter Tandberg, Magnus Løberg, Mette Kalager, Amyn Haji, Michael Bretthauer, Yuichi Mori: Real-Time Artificial Intelligence–Based Optical Diagnosis of Neoplastic Polyps during Colonoscopy, NEJM Evidence, vol. 1, no. 6 (April 2022) DOI: 10.1056/EVIDoa2200003
  13. Yosuke Minegishi, Shin-ei Kudo, Yuki Miyata, Tetsuo Nemoto, Kensaku Mori, Masashi Misawa, Showa University and Nagoya University AI research group(Corporate Authors: Yuichi Mori, Kentaro Mochida, Yoshika Akimoto, Misaki Ishiyama, Yohei Ogura, Masahiro Abe, Yuta Sato, Yushi Ogawa, Yasuharu Maeda, Kenta Tanaka, Katsuro Ichimasa, Hiroki Nakamura, Noriyuki Ogata, Tomokazu Hisayuki, Toyoki Kudo, Takemasa Hayashi, Kunihiko Wakamura, Hideyuki Miyachi, Toshiyuki Baba, Fumio Ishida, Hayato Itoh, Masahiro Oda): Comprehensive Diagnostic Performance of Real-Time Characterization of Colorectal Lesions using an Artificial Intelligence-Assisted System: a Prospective Study, Gastroenterology, vol. 163, issue 1, pp. 323-325.e3 (April 2022) DOI: 10.1053/j.gastro.2022.03.053, IF: 33.9
  14. Misaki Ishiyama, Shin-ei Kudo, Masashi Misawa, Yuichi Mori, Yasuharu Maeda, Katsuro Ichimasa, Toyoki Kudo, Takemasa Hayashi, Kunihiko Wakamura, Hideyuki Miyachi, Fumio Ishida, Hayato Itoh, Masahiro Oda, Kensaku Mori: Impact of the clinical use of artificial intelligence-assisted neoplasia detection for colonoscopy: a large-scale prospective, propensity score-matched study (with video), Gastrointestinal Endoscopy, vol.95, issue 1, pp. 155-163 (January 2021) DOI: 10.1016/j.gie.2021.07.022, IF: 10.4
  15. Hayato Itoh, Masahiro Oda, Kai Jiang, Yuichi Mori, Masashi Misawa, Shin-Ei Kudo, Kenichiro Imai, Sayo Ito, Kinichi Hotta, Kensaku Mori: Binary polyp-size classification based on deep-learned spatial information, International Journal of Computer Assisted Radiology and Surgery, vol. 16, pp. 1817–1828 (October 2021) DOI: 10.1007/s11548-021-02477-z, Nagoya Repository, SharedIt, IF: 2.9
  16. Shin-ei Kudo, Yuichi Mori, Usama M. Abdel-aal, Masashi Misawa, Hayato Itoh, Masahiro Oda, Kensaku Mori: Artificial intelligence and computer-aided diagnosis for colonoscopy: where do we stand now?, Translational Gastroenterology and Hepatology, vol. 6 (October 2021). DOI: 10.21037/tgh.2019.12.14
  17. Yuichi Mori, Shin-ei Kudo, Masashi Misawa, Kinichi Hotta, Ohtsuka Kazuo, Shoichi Saito, Hiroaki Ikematsu, Yutaka Saito, Takahisa Matsuda, Takeda Kenichi, Toyoki Kudo, Tetsuo Nemoto, Hayato Itoh, Kensaku Mori: Artificial intelligence-assisted colonic endocytoscopy for cancer recognition: a multicenter study, Endoscopy International Open, vol. 09, issue 07, pp. E1004-E1011 (July 2021) DOI: 10.1055/a-1475-3624
  18. Hayato Itoh, Masahiro Oda, Yuichi Mori, Masashi Misawa, Shin-Ei Kudo, Kenichiro Imai, Sayo Ito, Kinichi Hotta, Hirotsugu Takabatake, Masaki Mori, Hiroshi Natori, Kensaku Mori: Unsupervised colonoscopic depth estimation by domain translations with a Lambertian-reflection keeping auxiliary task, International Journal of Computer Assisted Radiology and Surgery, vol. 16, pp. 989–1001 (June 2021) DOI: 10.1007/s11548-021-02398-x, Nagoya Repository, SharedIt, IF: 2.9
  19. Masashi Misawa, Shin-ei Kudo, Yuichi Mori, Kinichi Hotta, Kazuo Ohtsuka, Takahisa Matsuda, Shoichi Saito, Toyoki Kudo, Toshiyuki Baba, Fumio Ishida, Hayato Itoh, Masahiro Oda, Kensaku Mori: Development of a computer-aided detection system for colonoscopy and a publicly accessible large colonoscopy video database (with video), Gastrointestinal Endoscopy, vol. 93, issue 4, pp. 960-967 (April 2021) DOI: 10.1016/j.gie.2020.07.060, IF: 9.4
  20. Shin-ei Kudo, Katsuro Ichimasa, Benjamin Villard, Yuichi Mori, Masashi Misawa, Shoichi Saito, Kinichi Hotta, Yutaka Saito, Takahisa Matsuda, Kazutaka Yamada, Toshifumi Mitani, Kazuo Ohtsuka, Akiko Chino, Daisuke Ide, Kenichiro Imai, Yoshihiro Kishida, Keiko Nakamura, Yasumitsu Saiki, Masafumi Tanaka, Shu Hoteya, Satoshi Yamashita, Yusuke Kinugasa, Masayoshi Fukuda, Toyoki Kudo, Hideyuki Miyachi, Fumio Ishida, Hayato Itoh, Masahiro Oda, Kensaku Mori: Artificial Intelligence System to Determine Risk of T1 Colorectal Cancer Metastasis to Lymph Node, Gastroenterology, vol. 160, no. 4, pp. 1075-1084.e2 (March 2021) DOI: 10.1053/j.gastro.2020.09.027, IF: 22.7
  21. Masashi Misawa, Shin-ei Kudo, Yuichi Mori, Yasuharu Maeda, Yushi Ogawa, Katsuro Ichimasa, Toyoki Kudo, Kunihiko Wakamura, Takemasa Hayashi, Hideyuki Miyachi, Toshiyuki Baba, Fumio Ishida, Hayato Itoh, Masahiro Oda, Kensaku Mori: Current status and future perspective on artificial intelligence for lower endoscopy, Digestive Endoscopy, vol. 33, issue 2, pp. 273-284 (January 2021) DOI: 10.1111/den.13847, IF: 7.6
  22. Hayato Itoh, Yukitaka Nimura, Yuichi Mori, Masashi Misawa, Shin-Ei Kudo, Kinichi Hotta, Kazuo Ohtsuka, Shoichi Saito, Yutaka Saito, Hiroaki Ikematsu, Yuichiro Hayashi, Masahiro Oda, Kensaku Mori: Robust endocytoscopic image classification based on higher-order symmetric tensor analysis and multi-scale topological statistics, International Journal of Computer Assisted Radiology and Surgery, vol. 15, pp. 2049–2059 (Decmber 2020) DOI: 10.1007/s11548-020-02255-3, Nagoya Repository, SharedIt, IF: 2.5
  23. Shin-ei Kudo, Masashi, Misawa, Yuichi Mori, Kinichi Hotta, Kazuo Ohtsuka, Hiroaki, Ikematsu, Yutaka Saito, Kenichi Takeda, Hiroki Nakamura, Katsuro Ichimasa, Tomoyuki Ishigaki, Naoya Toyoshima, Toyoki Kudo, Takemasa Hayashi, Kunihiko Wakamura, Toshiyuki Baba, Fumio Ishida, Haruhiro Inoue, Hayato Itoh, MasahiroOda, Kensaku Mori: Artificial Intelligence-assisted System Improves Endoscopic Identification of Colorectal Neoplasms, Clinical Gastroenterology and Hepatology, vol. 18, issue 8, pp. 1874-1881.e2 (July 2020) DOI: 10.1016/j.cgh.2019.09.009,IF: 11.4
  24. Yuichi Mori, Shin-ei Kudo, Masashi Misawa, Kenichi Takeda, Toyoki Kudo, Hayato Itoh, Masahiro Oda, Kensaku Mori: How Far Will Clinical Application of AI Applications Advance for Colorectal Cancer Diagnosis?, Journal of the Anus, Rectum and Colon, vol. 4, no. 2. pp. 47-50 (April 2020) DOI: 10.23922/jarc.2019-045
  25. Yuichi Mori, Shin-ei Kudo, Masashi Misawa, Kenichi Takeda,Toyoki Kudo, Hayato Itoh, Masahiro Oda, Kensaku Mori: Artificial Intelligence for Colorectal Polyp Detection and Characterization, Current Treatment Options in Gastroenterology, vol. 18, pp. 200–211, 2020. DOI: 10.1007/s11938-020-00287-x
  26. Yuichi Mori, Shin-ei Kudo, Masashi Misawa, Hayato Itoh, MasahiroOda, Kensaku Mori: Artificial intelligence for magnifying endoscopy, endocytoscopy, and confocal laser endomicroscopy of the colorectum, Techniques and Innovations in Gastrointestinal Endoscopy, vol. 22, issue 2, pp. 56-60 (April 2020) DOI: 10.1016/j.tgie.2019.150632
  27. Hayato Itoh, Holger Roth, Masahiro Oda, Masashi Misawa, Yuichi Mori, Shin-Ei Kudo, Kensaku Mori: Stable polyp-scene classification via subsampling and residual learning from an imbalanced large dataset, IET Healthcare Technology Letters, vol. 6, issue 6, pp. 237-242 (December 2019) DOI: 10.1049/htl.2019.0079, IF:2.1
  28. Shin-ei Kudo, Yuichi Mori, Masashi Misawa, Kenichi Takeda, Toyoki Kudo, Hayato Itoh, Masahiro Oda, Kensaku Mori: Artificial intelligence and colonoscopy: Current status and future perspectives, Digestive endoscopy, vol. 31, issue 4, pp. 363-371 (July 2019) DOI: 10.1111/den.13340, IF: 4.8
  29. Yuichi Mori, Shin‐ei Kudo, Hussein Ebaid Naeem Mohmed, Masashi Misawa, Noriyuki Ogata, Hayato Itoh, Masahiro Oda, Kensaku Mori: Artificial intelligence and upper gastrointestinal endoscopy: current status and future perspective, Digestive endoscopy, vol. 34, no. 4, pp.378-388 (July 2019) DOI: 10.1111/den.13317, IF: 4.8
  30. Yuichi Mori, Shin-ei Kudo, Masashi Misawa, Yutaka Saito, Hiroaki Ikematsu, Kinichi Hotta, Kazuo Ohtsuka, Fumihiko Urushibara, Shinichi Kataoka, Yushi Ogawa, Yasuharu Maeda, Kenichi Takeda, Hiroki Nakamura, Katsuro Ichimasa, Toyoki Kudo, Takemasa Hayashi, Kunihiko Wakamura, Fumio Ishida, Haruhiro Inoue, Hayato Itoh, Masahiro Oda, Kensaku Mori: Real-Time Use of Artificial Intelligence in Identification of Diminutive Polyps During Colonoscopy: A Prospective Study, Annals of Internal Medicine, vol. 169, no. 6, pp. 357-366 (September 2018) DOI: 10.7326/M18-0249, IF: 19.4
  31. Masashi Misawa, Shin-eiKudo, Yuichi Mori, Tomonari Cho, Shinichi Kataoka, Akihiro Yamauchi, Yushi Ogawa, Yasuharu Maeda, Kenichi Takeda, Katsuro Ichimasa, Hiroki, Nakamura, Yusuke Yagawa, Naoya Toyoshima, Noriyuki Ogata, Toyoki Kudo, Tomokazu Hisayuki, Takemasa Hayashi, Kunihiko Wakamura, Toshiyuki Baba, Fumio Ishida, Hayato Itoh, Holger Roth, Masahiro Oda, Kensaku Mori: Artificial Intelligence-Assisted Polyp Detection for Colonoscopy: Initial Experience, Gastroenterology, vol. 154, issue 8, pp. 2027-2029.e3 (June 2018) DOI: 10.1053/j.gastro.2018.04.003, IF: 19.8
  32. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Pattern recognition in multilinear space and its applications: mathematics, computational algorithms and numerical validations, Machin Vision and Applications, vol. 27, pp. 1259–1273 (September 2016) DOI: 10.1007/s00138-016-0806-2, SharedIt, IF: 2.0
  33. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Dimension Reduction and Construction of Feature Space for Image Pattern Recognition, Journal of Mathematical Imaging and Vision, vol. 56, issule 1, pp. 1-31 (Feburary 2016) DOI: 10.1007/s10851-015-0629-1, SharedIt, IF: 2.0

International Conference

  1. Tao Hu, Hayato Itoh, Masahiro Oda, Shinji Saiki, Koji Kamagata, Kei-ichi Ishikawa, Wataru Sako, Nobutaka Hattori, Shigeki Aoki, Kensaku Mori: Fully automated segmentation of substantia nigra towards longitudinal analysis of Parkinson’s Disease, Computer Assisted Radiology and Surgery - 38th International Congress and Exhibition (CARS 2024), Barcelona, Spain, 2024
  2. Ryo Toda, Hayato Itoh, Masahiro Oda, Yuichiro Hayashi, Yoshito Otake, Masahiro Hashimoto, Toshiaki Akashi, Shigeki Aoki, Kensaku Mori: Performance improvement for medical image classification model by using gradient-based analytical feature selection, Proc. SPIE Medical Imaging 2024: Computer-Aided Diagnosis (204/02/16-02/20), SPIE vol. 12927,12927-85, Calfornia, USA (2024/02/19)
  3. Tao Hu, Hayato Itoh, Masahiro Oda, Shinji Saiki, Nobutaka Hattori, Koji Kamagata, Shigeki Aoki, Kensaku Mori: Boosting substantia nigra segmentation from T2 weighted MRI via test-time normalization and distance-reweighted loss, Proc. SPIE Medical Imaging 2024: Computer-Aided Diagnosis (204/02/16-02/20), SPIE, vol. 12927, 12927-21, San Diego, Calfornia, USA (2024/02/20)
  4. Hayato Itoh, Masahiro Oda, Shinji Saiki, Koji Kamagata, Nobutaka Hattori, Shigeki Aoki, Kensaku Mori: Discriminant Analysis of Parkinson-diseases-related patterns in the substantia nigra by nonnegative feature expression of neuromelanin images, Computer Assisted Radiology and Surgery - 37th International Congress and Exhibition (CARS 2023) (2023/0620/-06/23), Munich, Germany (2023/6/21), International Journal of Computer Assisted Radiology and Surgery, vol. 18, suppl., pp. S27-S28 (2023)
  5. Ryo Toda, Hayato Itoh, Masahiro Oda, Yuichiro Hayashi, Yoshito Otake, Masahiro Hashimoto, Toshiaki Akashi, Shigeki Aoki, Kensaku Mori: Data-Driven COVID-19 Analysis bases on Three-Dimensional Attention Mechanisms, accepted to Computer Assisted Radiology and Surgery - 37th International Congress and Exhibition (CARS 2023) (2023/0620/-06/23), Munich, Germany (2023/6/22)
  6. Tao Hu, Hayato Itoh, Masahiro Oda, Shinji Saiki, Nobutaka Hattori, Koji Kamagata, Shigeki Aoki, Kensaku Mori: Priority Attention Network with Bayesian Learning for Fully Automatic Segmentation of Substantia Nigra from Neuromelanin MRI, Proc. SPIE Medical Imaging 2023: Image Processing (2023/02/19-02/23), SPIE vol. 12464, 124643G, San Diego, Calfornia, USA (2023/02/22)
  7. Tao Hu, Hayato Itoh, Masahiro Oda, Yuichiro Hayashi, Zhongyang Lu, Kensaku Mori, Nobutaka Hattori, Koji Kamagata, Shigeki Aoki: Improving Automated Substantia Nigra Segmentation Accuracy Using a Novel Test-time Normalization Method, 108th Scientific Assembly and Annual Meeting of the Radiological Society of North America (RSNA 2022), NREE-139, Online (2022/11/27-12/1)
  8. Hayato Itoh, Tao Hu, Masahiro Oda, Shinji Saiki, Koji Kamagata, Nobutaka Hattori, Shigeki Aoki, Kensaku Mori: Pattern Analysis of Substantia Nigra in Parkinson Disease by Fifth-Order Tensor Decomposition and Multi-sequence MRI, Proc. 3rd International Workshop on Multiscale Multimodal Medical Imaging (MMMI 2022) in conjunction with 25th MICCAI2022 (2022/9/18-9/22), LNCS vol. 13594, pp. pp 63–75, Singapore (2022/9/22)
  9. Tao Hu, Hayato Itoh, Masahiro Oda, Yuichiro Hayashi, Zhongyang Lu, Shinji Saiki, Nobutaka Hattori, Koji Kamagata, Shigeki Aoki, Kanako K. Kumamaru, Toshiaki Akashi, Kensaku Mori: Enhancing Model Generalization for Substantia Nigra Segmentation Using a Test-time Normalization-Based Method, 25th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI2022) (2022/9/18-9/22), LNCS vol. 13437,pp.736-744, Singapore (2022/9/20)
  10. Hayato Itoh, Masashi Misawa, Yuichi Mori, Shin-Ei Kudo, Masahiro Oda, Kensaku Mori: Positive-Gradient Weighted Object Activation Mapping: Analysis of Object Detector Towards Precise Colorectal-Polyp Localisation, Computer Assisted Radiology and Surgery - 36th International Congress and Exhibition (CARS 2022) (2022/6/7-6/11), Tokyo, Japan (2022/6/9)
  11. Kai Jiang, Hayato Itoh, Msahiro Oda, Taishi Okumura, Yuichi Mori, Masashi Misawa, Takemasa Hayashi, Shin-Ei. Kudo, Kensaku Mori: Gaussian Affinity and GIoU-based Loss for Perforation Detection and Localization from Colonoscopy Videos, Computer Assisted Radiology and Surgery - 36th International Congress and Exhibition (CARS 2022) (2022/6/7-6/11), Tokyo, Japan (2022/6/9)
  12. Hayato Itoh, Masahiro Oda, Shinji Saiki, Nobutaka Hattori, Koji Kamagata, Shigeki Aoki, Kensaku Mori: Substantia Nigra Analysis by Tensor Decomposition ofT2-weighted Images for Parkinson’s Disease Diagnosis, Medical Imaging 2022: Image Processing (in Person, 2022/2/20-2/24), SPIE vol. 12032, pp. 987-992, San Diego, Calfornia, USA/Online (Online, 2022/3/21-3/27)
  13. Tao Hu, Hayato Itoh, Masahiro Oda, Shinji Saiki, Nobutaka Hattori, Koji Kamagata, Shigeki Aoki, Kensaku Mori: Size-reweighted cascaded fully convolutional network for substantial nigra segmentation from T2 MRI, Medical Imaging 2022: Image Processing (in Person, 2022/2/20-2/24), SPIE vol. 12032, pp. 920-926, San Diego, Calfornia, USA/Online (Online, 2022/3/21-3/27)
  14. Eri Mochizuki, Haruka Sone, Hayato Itoh, Atsushi Imiya: Subspace Discrimination Method for Images Using Singular Value Decomposition, Proc. 16th International Symposium on Visual Computing (ISVC 2021) (2021/10/4-10/6), LNCS vol 13018. pp 287-298, Online (2021/10/6)
  15. Hayato Itoh, Masahiro Oda , Kai Jiang, Yuichi Mori, Masashi Misawa, Shin-Ei Kudo, Kenichiro Imai, Sayo Itoh, Kinichi Hotta, Kensaku Mori: Uncertainty Meets 3D-Spatial Feature in Colonoscopic Polyp-Size Determination, Joint MICCAI workshop 2020 AE-CAI/CARE/OR2.0, Strasbourg, France/Online (2021/9/27)
  16. Masahiro Oda, Hayato Itoh, Kiyohito Tanaka, Hirotsugu Takabatake, Masaki Mori, Hiroshi Natori, Kensaku Mori: Depth Estimation from Single-shot Monocular Endoscope Image Using Image Domain Adaptation And Edge-Aware Depth Estimation, Joint MICCAI workshops: AE-CAI/CARE/OR2.0, Strasbourg, France/Online (2021/9/27)
  17. Hayato Itoh, Masahiro Oda, Yuichi Mori, Masashi Misawa, Shin-ei Kudo, Kinnichi Hotta, Hirotsugu Takabatake, Masaki Mori, Hiroshi Natori, Kensaku Mori: Single-shot three-dimensional reconstruction for colonoscopic image analysis, Medical Imaging: Image-Guided Procedures, Robotic Interventions, and Modeling (2021/2/15-19), SPIE vol. 11598, pp. 90-95, Online (2021/2/15)
  18. Kai Jiang, Hayato Itoh, Masahiro Oda, Taishi Okumura, Yuichi Mori, Masashi Misawa, Takemasa Hayashi, Shin-Ei Kudo, Kensaku Mori: Dense-layer-based YOLO-v3 for detection and localization of colon perforations, Medical Imaging 2021: Computer-Aided Diagnosis (2021/2/15-19), SPIE vol. 11597, pp. 296-301, Online (2021/2/15)
  19. Zhongyang Lu, Masahiro Oda, Yuichiro Hayashi, Tao Hu, Hayato Itoh, Takeyuki Watadani, Osamu Abe, Masahiro Hashimoto, Masahiro Jinzaki, Kensaku Mori: Extremely imbalanced subarachnoid hemorrhage detection based on DenseNet-LSTM network with class-balanced loss and transfer learning, Medical Imaging 2021: Computer-Aided Diagnosis (2021/2/15-19), SPIE vol. 11597, pp. 464-469, Online (2021/2/15)
  20. Hirohisa Oda, Yuichiro Hayashi, Takayuki Kitasaka, Yudai Tamada, Aitaro Takimoto, Akinari Hinoki, Hiroo Uchida, Kojiro Suzuki, Hayato Itoh, Masahiro Oda, Kensaku Mori: Intestinal region reconstruction of ileus cases from 3D CT images based on graphical representation and its visualization, Medical Imaging 2021: Computer-Aided Diagnosis (2021/2/15-19), SPIE vol. 11597, pp. 388-395, Online (2021/2/15)
  21. Hayato Itoh, Masahiro Oda, Kai Jiang, Yuchi Mori, Masashi Misawa, Shin-Ei Kudo, Kenichiro Imai, Sayo Ito, Kinichi Hotta, Kensaku Mori: Binary Polyp-Size Classification based on Deep-Learning Estimation of Spatial Information, Computer Assisted Radiology and Surgery - 35nd International Congress and Exhibition (CARS 2021) (2021/6/21-6/25), Munich, Germany/Online (2021/6/22)
  22. Hirohisa Oda, Yuichiro Hayashi, Takayuki Kitasaka, Yudai Tamada, Aitaro Takimoto, Akinari Hinoki, Hiroo Uchida, Kojiro Suzuki, Hayato Itoh, Masahiro Oda, Kensaku Mori: Intestine segmentation combining Watershed transformation and machine learning-based distance map estimation, Computer Assisted Radiology and Surgery - 35th International Congress and Exhibition (CARS 2021) (2021/6/21-6/25), International Journal of Computer Assisted Radiology and Surgery, vol.16, suppl., pp.S89-90, Munich, Germany/Online (2021/6/24)
  23. Kai Jiang, Hayato Itoh, Masahiro Oda, Taishi Okumura, Yuichi Mori, Masashi Misawa, Takemasa Hayashi, Shin-Ei Kudo, Kensaku Mori: Experimental evaluation of loss functions in YOLO-v3 training for the perforation detection and localization in colonoscopic videos, Computer Assisted Radiology and Surgery - 35th International Congress and Exhibition (CARS 2021) (2021/6/21-6/25), International Journal of Computer Assisted Radiology and Surgery, vol.16, suppl., pp.S74-75, Munich, Germany/Online (2021/6/22)
  24. Hayato Itoh, Zhongyang Lu, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-ei Kudo, Kensaku Mori: Visualising decision-reasoning regions in computer-aided pathological pattern diagnosis of endoscytoscopic images based on CNN weights analysis, Proc. Medical Imaging 2020: Computer-Aided Diagnosis (2020/2/15-2/20) , SPIE vol. 11314, pp. 761-768, Houston, Texas, USA (2020/2/17)
  25. Hirohisa Oda, Kohei Nishio, Takayuki Kitasaka, Hizuru Amano, Aitaro Takimoto, Hiroo Uchida, Kojiro Suzuki, Hayato Itoh, Masahiro Oda, Kensaku Mori: Visualizing intestines for diagnostic assistance of ileus based on intestinal region segmentation from 3D CT images, Proc. Medical Imaging 2020: Computer-Aided Diagnosis (2020/2/15-2/20) , SPIE vol. 11314, pp. 728-735, Houston, Texas, USA (2020/2/17)
  26. Kensaku Mori, Yuta Hibi, Yuichiro Hayashi, Masahiro Oda, Kazunari Misawa, Hayato Itoh: How Does Graphical Convolutional Neural Network Work for Anatomical Labeling of Blood Vessels Extracted From CT Images?, 106th Scientific Assembly and Annual Meeting of the Radiological Society of North America (RSNA 2020), NI112-ED-X, Online (2020/11/29-12/5)
  27. Kohei Nishio, Hirohisa Oda, Takayuki Kitasaka, Yudai Tamada, Hizuru Amano, Aitaro Takimoto, Kosuke Chiba, Yuichiro Hayashi, Hayato Itoh, Masahiro Oda, Akinari Hinoki, Hiroo Uchida, Kensaku Mori: Virtual cleansing by unpaired image translation of intestines for detecting obstruction, Computer Assisted Radiology and Surgery - 34th International Congress and Exhibition (CARS 2020) (2020/6/23-6/27), International Journal of Computer Assisted Radiology and Surgery, vol.15, suppl., pp.S21-22, Munich, Germany (2020/6/26)
  28. Hayato Itoh, Yuichi Mori, Masashi Misawa, Shin–Ei Kudo, K. Hotta, K. Ohtsuka, S. Saito, Y. Saito, H. Ikematsu, Yuichiro Hayashi, Masahiro Oda, Kensaku Mori: Development of a robust endocytoscopic-image classification method towards the construction of practical CAD system in endocytoscopy - from the viewpoint of generalisation ability for non-specific hospital diagnosis, Computer Assisted Radiology and Surgery - 34th International Congress and Exhibition (CARS 2020) (2020/6/23-6/27), Munich, Germany (20206/22)
  29. Hayato Itoh, Atsushi Imiya: Multilinear Subspace Method Based on Geodesic Distance for Volumetric Object Classification, Proc. 18th International Conference on Computer Analysis of Images and Patterns (CAIP 2019) (2019/9/2-9/6), Lecture Notes in Computer Science, vol. 11678, pp. 672-683, Salerno, Italia (2019/9/3)
  30. Hayato Itoh, Holger R. Roth, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-ei Kudo, Kensaku Mori: Polyp-size classification with RGB-D features for colonoscopy, Medical Imaging 2019: Computer-Aided Diagnosis (2019/2/16-2/21), SPIE vol. 10950, pp. 282-288, San Diego, California, USA (2019/2/18)
  31. Hirohisa Oda, Kohei Nishio, Takayuki Kitasaka, Benjamin Villard, Hizuru Amano, Kosuke Chiba, Akinari Hinoki, Hiroo Uchida, Kojiro Suzuki, Hayato Itoh, Masahiro Oda, Kensaku Mori: Spaciousness Filters for Non-contrast CT Volume Segmentation of the Intestine Region for Emergency Ileus Diagnosis, Proc. Workshop on Clinical Image-Based Procedures and International Workshop on Uncertainty for Safe Utilization of Machine Learning in Medical Imaging (CLIP/UNSURE 2019), Lecture Notes in Computer Science, vol 11840, pp. 104-114, Shenzhen, China (2019/10/17)
  32. Chenglong Wang, Yuichiro Hayashi, Masahiro Oda, Hayato Itoh, Takayuki Kitasaka, Alejandro F. Frangi, Kensaku Mori: Tubular Structure Segmentation Using Spatial Fully Connected Network with Radial Distance Loss for 3D Medical Images, Proc. 22nd International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2019) (2019/10/13/-10/17), Lecture Notes in Computer Science, vol 11769, pp. 348-356, Shenzhen, China (2019/10/15)
  33. Hayato Itoh, Holger Roth, Masahiro Oda, Masashi Misawa, Yuichi Mori, Shin-Ei Kudo, Kensaku Mori: Stable Polyp-Scene Classification via Subsampling and Residual Learning from an Imbalanced Large Dataset, Joint MICCA Workshops: MIAR & AE-CAI & CARE 2019, Shenzhen, China (2019/10/13)
  34. Hayato Itoh, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-Ei Kudo, Kensaku Mori: Polyp-Size Determination Method using Short Colonoscopic Video Clip Information, Computer Assisted Radiology and Surgery - 33rd International Congress and Exhibition (CARS 2019) (2019/6/18-6/21), International Journal of Computer Assisted Radiology and Surgery, 14(1), pp. s88-89, Rennes, France (2019/6/20)
  35. Cheng Wang, Masahiro Oda, Yuichiro Hayashi, Takayuki Kitasaka, Hayato Itoh, Hirotoshi Honma, Hirotsugu Takabatake, Masaki Mori, Hiroshi Natori, Kensaku Mori: Evaluation on reconstruction accuracy of visual SLAM based bronchoscope tracking, Computer Assisted Radiology and Surgery - 33rd International Congress and Exhibition (CARS 2019) (2019/6/18-6/21), International Journal of Computer Assisted Radiology and Surgery, vol.14, suppl., pp.S24-25, Rennes, France (2019/6/20)
  36. Benjamin Villard, Hayato Itoh, Katsuro Ichimasa, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-Ei Kudo, Kensaku Mori: Artificial neural network for the prediction of colorectal lymph node metastasis, Computer Assisted Radiology and Surgery - 33rd International Congress and Exhibition (CARS 2019) (2019/6/18-6/21), Rennes, France (2019/6/20)
  37. Shintaro Morimitsu, Hayato Itoh, Takuya Ozawa, Hirohisa Oda, Takayuki Kitasaka, Takaaki Sugino, Yuichiro Hayashi, Nobuyoshi Takeshita, Masaaki Ito, Masahiro Oda, Kensaku Mori: Automatic segmentation of attention-aware artery region in laparoscopic colorectal surger, Computer Assisted Radiology and Surgery - 33rd International Congress and Exhibition (CARS 2019) (2019/6/18-6/21), International Journal of Computer Assisted Radiology and Surgery, vol.14, suppl., pp.s41-42, Rennes, France (2019/6/20)
  38. Xiaotian Zhao, Hirohisa Oda, Shota Nakamura, Yuichiro Hayashi, Hayato Itoh, Masahiro Oda, Kensaku Mori: Investigation of extracting interlobular septa with Hessian analysis and radial structure tensor combined with roundness error in micro-CT volume, Proc. International Forum on Medical Imaging in Asia (IFMIA 2019) (2019/1/6-1/9), SPIE vol. 11050, pp. 243-248, Singapore, Singapore (2019/01/08)
  39. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Distances Between Tensor Subspaces, Proc. First International Conference on Applications of Intelligent Systems (APPIS 2018) (2018/1/8-1/12), Frontiers in Artificial Intelligence and Applications vol. 310, pp. 50-59, Las Palmas de Gran Canaria, Spain (2018/1/11)
  40. Kaori Tanji, Hayato Itoh, Atsushi Imiya: Application of Directional Statistics to Classification of Three-Channel Colour Images, Proc. First International Conference on Applications of Intelligent Systems (APPIS 2018) (2018/1/8-1/12), Frontiers in Artificial Intelligence and Applications vol. 310, pp. 60-69, Las Palmas de Gran Canaria, Spain, (2018/1/10)
  41. Kento Hosoya, Ryo Sasaki, Kaori Tanji, Hayato Itoh, Atsushi Imiya: Variational Method for Multiresolution Image Registration, Proc. First International Conference on Applications of Intelligent Systems (APPIS 2018) (2018/1/8-1/12), Frontiers in Artificial Intelligence and Applications vol. 310, pp. 157-168, Las Palmas de Gran Canaria, Spain (2018/1/10)
  42. Hayato Itoh, Atsushi Imiya: Discrimination of Volumetric Shapes Using Orthogonal Tensor Decomposition, Proc. International Workshop on Shape in Medical Imaging (ShapeMI 2018) in conjunction with MICCAI 2018, Lecture Notes in Computer Science vol. 11167, pp.277-290, Granada, Spain (2018/9/20)
  43. Hayato Itoh, Holger R. Roth, Le Lu, Masahiro Oda, Masashi Misawa, Yuichi Mori, Shin-ei Kudo, Kensaku Mori: Towards Automated Colonoscopy Diagnosis: Binary Polyp Size Estimation via Unsupervised Depth Learning, Proc. 21st International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2018) (2018/9/16-9/20), Lecture Notes in Computer Science, vol. 11071, pp. 611-619, Granada, Spain (2018/9/18)
  44. Hayato Itoh, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-ei Kudo, Kensaku Mori: Discriminative Feature Selection by Optimal Manifold Search for Neoplastic Image Recognition, Proc. 2nd International Workshop on Compact and Efficient Feature Representation and Learning in Computer Vision (CEFRL 2018) in conjunction with ECCV 2018, Lecture Notes in Computer Science, vol. 11132, pp. 534-549, Munich, Germany (2018/9/9)
  45. Hayato Itoh, Holger R. Roth, Masashi Misawa, Yuichi Mori, Masahiro Oda, Shin-ei Kudo, Kensaku Mori: Polyp detection in colonoscopic videos by using spatio-temporal feature, International Journal of Computer Assisted Radiology and Surgery, vol.13, suppl., pp.s97-98, Computer Assisted Radiology and Surgery - 32nd International Congress and Exhibition (CARS 2018) (2018/6/20-6/23), Berlin, Germany (2018/06/22)
  46. Hayato Itoh, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-ei Kudo, Kensaku Mori: Cascade classification of endocytoscopic images of colorectal lesions for automated pathological diagnosis, Medical Imaging 2018: Computer-Aided Diagnosis (2018/2/10-2/15), SPIE vol. 10575, pp. 269 -274, Houston, Texas, USA (2018/2/14)
  47. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Multilinear Methods for Spatio-Temporal Image Recognition, Proc. 17th International Conference on Computer Analysis of Images and Patterns (CAIP 2017) (2017/8/22-8/24), Lecture Notes in Computer Science, vol.10424, pp. 148-159, Ystad, Sweden (2017/8/22)
  48. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Analysis of Multilinear Subspaces Based on Geodesic Distance. Proc. 17th International Conference on Computer Analysis of Images and Patterns (CAIP 2017) (2017/8/22-8/24), Lecture Notes in Computer Science, vol.10424, pp. 384-396, Ystad, Sweden (2017/8/23)
  49. Tomoya Kato, Hayato Itoh, Atsushi Imiya: Motion Language of Stereo Image Sequence, Proc. Joint workshop on Computer Vision in Vehicle Technology and Autonomous Driving Challenge in conjuction with CVPR 2017, pp. 1211-1218, Honolulu, Hawaii, USA (2017/7/21)
  50. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Fast Approximate Karhunen-Loève Transform for Three-Way Array Data, Proc. Second International Workshop on Robust Subspace Learning and Applications in Computer Vision in conjunction with ICCV 2017, pp. 1827-1834, Venice, Italia (2017/10/28)
  51. Kaori Tanji, Atsushi Imiya, Hayato Itoh, Hiroaki Kuze, Naohiro Manago: Linear Data Compression of Hyperspectral Images. Proc. 6th Color and Photometry in Computer Vision Wokshop in conjuction with ICCV 2017, pp. 3001-3007, Venice, Italia (2017/10/29)
  52. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Approximation of N-Way Principal Component Analysis for Organ Data, Proc. Workshop on Mathematical and Computational Methods in Biomedical Imaging and Image Analysis (MCBMIIA 2016) in conjunction with ACCV 2016, Lecture Notes in Computer Science, vol.10118, pp. 16-31, Taipei, Taiwan (2017/11/24)
  53. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Relaxed Optimisation for Tensor Principal Component Analysis and Applications to Recognition, Compression and Retrieval of Volumetric Shapes, Proc. Imaging, Vision and Learning Based on Optimization and PDEs (IVLOPDE 2016) (2016/8/29-9/1), pp. 165-200, Bergen, Norway (2016/8/30)
  54. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Volumetric Image Pattern Recognition Using Three-Way Principal Component Analysis, Proc. International Workshop on Spectral and Shape Analysis in Medical Imaging (SeSAMI 2016), Lecture Notes in Computer Science, vol.10126, pp. 103-117, Athens, Greece (2016/10/21)
  55. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Mathematical Aspects of Tensor Subspace Method. Proc. Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR) (S+SSPR 2016) (2016/11/30-12/2), Lecture Notes in Computer Science, vol. 10029, pp. 37-48, Mérida, Mexico (2016/12/2)
  56. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Classification of Volumetric Data Using Multiway Data Analysis. Proc. Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR) (S+SSPR 2016) (2016/11/30-12/2), Lecture Notes in Computer Science, vol. 10029, pp. 231-240, Mérida, Mexico (2016/12/1)
  57. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Discriminative Properties in Directional Distributions for Image Pattern Recognition, Proc. 7th Pacific Rim Symposium on Image and Video Technology (PSIVT 2015) (2015/11/25-11/27), Lecture Notes in Computer Science, vol. 9431, pp. 617-630, Auckland, New Zealand (2015/11/27)
  58. Shum Inagaki, Hayato Itoh, Atsushi Imiya: Simultaneous Frame-rate Up-conversion of Image and Optical Flow Sequences, Proc. 10th International Conference on Computer Vision Theory and Applications (VISAPP 2015) (2015/3/11-3/14), pp. 68-75, Berlin, Germany (2015/3/12)
  59. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Low-Dimensional Tensor Principle Component Analysis, Proc. 16th International Conference on Computer Analysis of Images and Patterns (CAIP 2015) (2015/9/2-9/4), Lecture Notes in Computer Science, vol.9256, pp. 715-726, Valletta, Malta (2015/9/4)
  60. Tomoya Kato, Hayato Itoh, Atsushi Imiya: Optical Flow Computation with Locally Quadratic Assumption, Proc. 16th International Conference on Computer Analysis of Images and Patterns (CAIP 2015) (2015/9/2-9/4), Lecture Notes in Computer Science, vol.9256, pp. 223-234, Valletta, Malta (2015/9/2)
  61. Shun Inagaki, Hayato Itoh, Atsushi Imiya: Variational Multiple Warping for Cardiac Image Analysis, Proc. 16th International Conference on Computer Analysis of Images and Patterns (CAIP 2015) (2015/9/2-9/4), Lecture Notes in Computer Science, vol.9257, pp. 749-759, Valletta, Malta (2015/9/4)
  62. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Global Volumetric Image Registration Using Local Linear Property of Image Manifold, Proc. Workshop on Big data in 3D Computer Vision in conjunction with ACCV 2014, Lecture Notes in Computer Science, vol.9008, 238-253, Singapore, Singapore (2014/11/1)
  63. Shun Inagaki, Hayato Itoh, Atsushi Imiya: Multiple Alignment of Spatiotemporal Deformable Objects for the Average-Organ Computation, Proc. 7th Workshop on Non-Rigid Shape Analysis and Deformable Image Alignment (NORDIA'14) in conjunction with ECCV2014, Lecture Notes in Computer Science, vol.8928, pp. 353-366, Zurich, Switzerland (2014/9/12)
  64. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Two-Dimensional Global Image Registration Using Local Linear Property of Image Manifold, Proc. 22nd International Conference on Pattern Recognition (ICPR 2014), pp. 3862-3867, Stockholm, Sweden (2014/8/24-8/28)
  65. Hayato Itoh, Shun Inagaki, Ming-Ying Fan, Atsushi Imiya, Kazuhiko Kawamoto, Tomoya Sakai: Local Affine Optical Flow Computation, Proc. PSIVT Workshop on Geometric Computation for Computer Vision, Lecture Notes in Computer Science, vol.8334, pp 203-215, Guanajuato, México (2013/10/29)
  66. Hayato Itoh, Tomoya Sakai, Kazuhiko Kawamoto, Atsushi Imiya: Global Image Registration Using Random Projection and Local Linear Method, Proc. 15th International Conference on Computer Analysis of Images and Patterns (CAIP2013) (2013/8/27-8/29), Lecture Notes in Computer Science, vol.8047, pp 564-571, York, UK (2013/8/28)
  67. Hayato Itoh, Tomoya Sakai, Kazuhiko Kawamoto, Atsushi Imiya: Topology-Preserving Dimension-Reduction Methods for Image Pattern Recognition, Proc. 18th Scandinavian Conference on Image Analysis (SCIA 2013), Lecture Notes in Computer Science, vol.7944, pp. 195-204, Espoo, Finland (2013/6/17-6/20)
  68. Hayato Itoh, Tomoya Sakai, Kazuhiko Kawamoto, Atsushi Imiya: Dimension Reduction Methods for Image Pattern Recognition, Proc. 2nd International Workshop on Similarity-Based Pattern Analysis and Recognition (SIMBAD 2013), Lecture Notes in Computer Science, vol.7953, pp. 26-42, York, UK (2013/7/3-7/5)
  69. Hayato Itoh, Shuang Lu, Tomoya Sakai, Atsushi Imiya: Interpolation of Reference Images in Sparse Dictionary for Global Image Registration, Proc. 8th International Symposium on Visual Computing (ISVC 2012) (2012/7/16-7/18), Lecture Notes in Computer Science, vol.7432 pp. 657-667, Rethymnon, Crete, Greece (2012/7/16)
  70. Masaki Narita, Atsushi Imiya, Hayato Itoh: Edge Detection and Smoothing-Filter of Volumetric Data. Proc. 8th International Symposium on Visual Computing (ISVC 2012) (2012/7/16-7/18), Lecture Notes in Computer Science, vol.7432, pp. 489-498, Rethymnon, Crete, Greece (2012/7/16)
  71. Tomoya Sakai, Haruhiko Nishiguchi, Hayato Itoh, Atsushi Imiya: Bifurcation of Segment Edge Curves in Scale Space, Proc. 3rd International Conference on Scale Space and Variational Methods in Computer Vision (SSVM 2011), Lecture Notes in Computer Science, vol.6667, pp.302-313, Ein-Gedi, Israe (2011/5/29-6/2)
  72. Hayato Itoh, Shuang Lu, Tomoya. Sakai, Atsushi Imiya: Global Image Registration by Fast Random Projection, Proc. 7th International Symposium on Visual Computing (ISVC 2011) (2011/9/26-9/27), Lecture Notes in Computer Science, Lecture Notes in Computer Science, vol.6938, pp.23-32, Las Vegas, Nevada, USA (2011/9/26)
  73. Tomoya Sakai, Hayato Itoh, Atsushi Imiya: Multi-label classification for image annotation via sparse similarity voting, Proc. 3rd International Workshop on Subspace Methods (Subspace 2010) in conjunction with ACCV2010, Lecture Notes in Computer Science, vol.6469(2), pp.344-353, Queenstown, New Zealand (2011/11/9)

Annual Meeting / Symposium

  1. 小野坂 捺, 伊東 隼人, 小田 昌宏, 三澤 将史, 森 悠一, 工藤 進英, 森 健策: 教師なし深層学習による大腸3次元復元のためのデータセット構築, 第2回JAMIT若手医用画像工学シンポジウム(SAMIT2024) 予稿集, SO2-4, p.33, 福岡大学中央図書館 多目的ホール (2024/9/21)
  2. 小野坂 捺, 伊東 隼人, 小田 昌宏, 三澤 将史, 森 悠一, 工藤 進英, 森 健策: 大腸内視鏡動画像を用いた3次元復元に関する初期的検討, 第43回日本医用画像工学会大会（JAMIT2024) 2024年8月5日-8月7日, 第43回日本医用画像工学会大会予稿集, OP18-5, pp.280-281, 一橋講堂 一橋大学 学術総合センター内 (2024/8/7)
  3. 遠田 涼，伊東 隼人，小田 昌宏，林 雄一郎，大竹 義人，橋本 正弘，明石 敏昭，青木 茂樹，森 健策: Attention 機構を有する CNN の重み解析による重要病変部特定に関する試み, JAMIT若手医用画像工学シンポジウム(SAMIT2023) 予稿集, p.7, 筑波大学 健康医科学イノベーション棟 (2023/9/30)
  4. 宮﨑 琳太郎，林 雄一郎，伊東 隼人，小田 昌宏, 森 健策: 八分木臓器モデルにおける変形操作に応じた動的局所細分化, JAMIT若手医用画像工学シンポジウム(SAMIT2023) 予稿集, pp.20-21, 筑波大学 健康医科学イノベーション棟 (2023/9/30)
  5. 伊東 隼人，小田 昌宏, 斉木 臣二, 服部 信孝, 鎌形 康司, 青木 茂樹, 森 健策: 神経メラニン画像を利用した黒質緻密部分類に関する初期的検討, 第42回日本医用画像工学会大会（JAMIT 2023) 2023年7月27日(木)-7月29日(土), 第42回日本医用画像工学会大会予稿集, OP14-4, pp.231-232, 大阪大学中之島センター (2023/7/29）
  6. 遠田 涼，伊東 隼人, 小田 昌宏，林 雄一郎，大竹 義人 橋本 正弘，明石 敏昭，青木 茂樹，森 健策: 2.5 次元特徴抽出及び 3 次元特徴選択による COVID-19 自動分類モデルの汎化性能に関する検討, 第42回日本医用画像工学会大会（JAMIT 2023) 2023年7月27日(木)-7月29日(土), 第42回日本医用画像工学会大会予稿集, OP12-4, pp.209-210, 大阪大学中之島センター (2023/7/28）
  7. 伊東 隼人，小田 昌宏, 斉木 臣二, 服部 信孝, 鎌形 康司, 青木 茂樹, 森 健策: テンソル分解を用いた黒質緻密部の3次元パターン表現に関する初期的検討, 第41回日本医用画像工学会大会（JAMIT 2022) 2022年7月29日(金)-7月31日(日), 第41回日本医用画像工学会大会予稿集, OP6-4, pp.124-125, 名古屋大学東山キャンパス豊田講堂 (2022/7/30）
  8. Zhongyang Lu, Masahiro Oda,1, Yuichiro Hayashi, Tao Hu, Hayato Itoh, Takeyuki Watadani, Osamu Abe，Kensaku Mori: A Novel Centroid-attention based Hybrid Model for Subarachnoid Hemorrhage Classification on Imbalanced Data, 第41回日本医用画像工学会大会（JAMIT 2022) 2022年7月29日(金)-7月31日(日), 第41回日本医用画像工学会大会予稿集,OP3-5, pp.104-105, 名古屋大学東山キャンパス豊田講堂 (2022/7/29）
  9. 伊東 隼人，潘 冬平，小澤 卓也，小田 昌宏, 竹下 修由, 伊藤 雅昭, 森 健策: 大規模腹腔鏡動画像データベース構築に向けたアノテーションツール開発, 第30回日本コンピュータ外科学会大会 (JSCAS 2021) 2021年11月21日(日)-23日(火), 日本コンピュータ外科学会誌, vol.23, no.4, pp.243-244, 21(5)-1, つくば国際会議場 (2021/11/22)
  10. 伊東 隼人, 小田 昌宏, 森 悠一, 三澤 将史, 工藤 進英, 森 健策: ピットパターン特徴量の解析に向けた超拡大内視鏡画像の再構成法に関する初期的検討, 第40回日本医用画像工学会大会（JAMIT 2021) 2021年10月13日(水)-10月15日(金), 第40回日本医用画像工学会大会予稿集, P3-12, pp.309-317, 慶應義塾大学 日吉キャンパス 協生館/オンライン開催 (2021/10/14)
  11. Kai Jiang, Hayato Itoh, Masahiro Oda, Taishi Okumura, Yuichi Mori, Masashi Misawa, Takemasa Hayashi, Shin-Ei Kudo, Kensaku Mori: Synthesized Perforation Detection from Endoscopy Videos Using Model Training with Synthesized Images by GAN, 第40回日本医用画像工学会大会（JAMIT 2021) 2021年10月13日(水)-10月15日(金), 第40回日本医用画像工学会大会予稿集, P2-12, pp.223-228, 慶應義塾大学 日吉キャンパス 協生館/オンライン開催 (2021/10/14)
  12. Zhongyang Lu，Masahiro Oda，Yuichiro Hayashi，Tao Hu，Hayato Itoh，Takeyuki Watadani，Osamu Abe, Masahiro Hashimoto, Masahiro Jinzaki, Kensaku Mori: Self-attention Class Balanced DenseNet_LSTM framework for Subarachnoid Hemorrhage CT image Classification on Extremely Imbalanced Brain CT Dataset, 第40回日本医用画像工学会大会（JAMIT 2021) 2021年10月13日(水)-10月15日(金), 第40回日本医用画像工学会大会予稿集, P1-02, pp.69-75, 慶應義塾大学 日吉キャンパス 協生館/オンライン開催 (2021/10/13)
  13. 伊東 隼人, 三澤 将史，森 悠一，小田 昌宏，工藤 進英, 森 健策: SUN database : 大腸ポリープ自動検出器の精度評価に向けた試験用画像, 第29回日本コンピュータ外科学会大会 (JSCAS 2020) 2020年11月22日(日)-23日(月), 日本コンピュータ外科学会誌, vol.22, no.4, 20(Ⅹ)-1, pp.346-347, Online (2020/11/23)
  14. 凱 蒋, 伊東隼人，小田 昌宏，奥村 大志，森 悠一，三澤 将史，林 武雅，工藤 進英，森 健策: Preliminary study of Loss-Function Design for Detection and Localization of Perforations with YOLO-v3 in Colonoscopic Images, 第29回日本コンピュータ外科学会大会 (JSCAS 2020) 2020年11月22日(日)-23日(月), 日本コンピュータ外科学会誌, vol.22, no.4, 20(Ⅹ)-2, pp.348-349, Online (2020/11/23)
  15. 屠 芸豪, 伊東 隼人，小澤 卓也，小田 昌宏, 竹下 修由，伊藤 雅昭，森 健策: 腹腔鏡動画像用オンラインアノテーションツールの開発, 第29回日本コンピュータ外科学会大会 (JSCAS 2020) 2020年11月22日(日)-23日(月), 日本コンピュータ外科学会誌, vol.22, no.4, 20(Ⅴ)-5, pp.306-307, Online (2020/11/22)
  16. 小田 紘久, 林 雄一郎, 北坂 孝幸，玉田 雄大,滝本 愛太朗，檜 顕成, 内田 広夫，鈴木 耕次郎, 伊東 隼人，小田 昌宏，森 健策: 腸閉塞およびイレウスの診断支援システムにおける距離マップの導入, 第29回日本コンピュータ外科学会大会 (JSCAS 2020) 2020年11月22日(日)-23日(月), 日本コンピュータ外科学会誌, vol.22, no.4, 20(Ⅱ)-3, pp.282-284, Online (2020/11/22)
  17. 屠 芸豪, 伊東 隼人, 小澤 卓也, 小田 昌宏, 竹下 修由, 伊藤 雅昭, 森 健策: 腹腔鏡手術動画像データベース構築に向けたリモートアノテーションツールのプロトタイプ開発, 第39回日本医用画像工学会大会（JAMIT 2020) 2020年9月17日(木)-9月19日(土), 第39回日本医用画像工学会大会予稿集, P5-23, pp.611-615, オンライン開催 (2020/9/19)
  18. 伊東 隼人, 小田 昌宏, 森 悠一, 三澤 将史, 工藤 進英, 堀田 欣一, 高畠 博嗣, 森 雅樹, 名取 博, 森 健策: 大腸内視鏡のための教師なし深度画像推定法における補助タスク検討: 第39回日本医用画像工学会大会（JAMIT 2020) 2020年9月17日(木)-9月19日(土), 第39回日本医用画像工学会大会予稿集, P5-14, pp.563-568, オンライン開催 (2020/9/19)
  19. 日比 裕太, 林 雄一郎, 北坂 孝幸, 伊東 隼人, 小田 昌宏, 三澤 一成, 森 健策: 広範囲の隣接関係を考慮したグラフニューラルネットワークを用いた腹部動脈血管名自動命名の検討: 第39回日本医用画像工学会大会（JAMIT 2020) 2020年9月17日(木)-9月19日(土), 第39回日本医用画像工学会大会予稿集, P2-18, pp.268-271, オンライン開催 (2020/9/18)
  20. Zhongyang Lu, Masahiro Oda, Yuichiro Hayashi, Tao Hu, Hayato Itoh，Takeyuki Watadani，Osamu Abe，Masahiro Hashimoto，Masahiro Jinzaki，Kensaku Mori: A study on Subarachnoid Hemorrhage automatic detection utilized Transfer Learning on extremely imbalanced brain CT datasets, 第39回日本医用画像工学会大会（JAMIT 2020) 2020年9月17日(木)-9月19日(土), 第39回日本医用画像工学会大会予稿集, P1-20, pp.168-172, オンライン開催 (2020/9/17)
  21. Kai Jiang, Hayato Itoh, Masahiro Oda, Taishi Okumura, Yuichi Mori, Masashi Misawa, Takemasa Hayashi, Shin-Ei Kudo, Kensaku Mori: Preliminary Study of Perforation Detection and Localization for Colonoscopy Video, 第39回日本医用画像工学会大会（JAMIT 2020) 2020年9月17日(木)-9月19日(土), 第39回日本医用画像工学会大会予稿集, P1-15, pp.142-147, オンライン開催 (2020/9/17)
  22. 伊東 隼人, 森 悠一, 三澤 将史, 小田 昌宏, 工藤 進英, 森 健策: 超拡大大腸内視鏡画像における施設間データ分布の差異を考慮した分類法に関する初期的検討, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vol.21, no.4 19(XIV)‒4, pp.332-333, 東京大学本郷キャンパス 工学部2号館 (2019/11/24)
  23. 西尾 光平, 小田 紘久, 千馬 耕亮, 北坂 孝幸, 林 雄一郎, 伊東 隼人, 小田 昌宏, 檜 顕成, 内田 広夫, 森 健策: 小児腸閉塞患者のCT像における電子洗浄手法の評価, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vol.21, no.4 19(XIII)‒3, pp.321, 東京大学本郷キャンパス 工学部2号館 (2019/11/24)
  24. 小澤 卓也, 小田 紘久, 伊東 隼人, 北坂 孝幸, 林 雄一郎, 小田 昌宏, 三澤 一成, 竹下 修由, 伊藤 雅昭, 森 健策: 生成型学習による腹腔鏡ビデオ自動認識のための画像生成システムの開発, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vol.21, no.4 19(VIII)‒4, pp.284-285, 東京大学本郷キャンパス 工学部2号館 (2019/11/23)
  25. 御手洗 翠, 小田 紘久, 杉野 貴明, 守谷 享泰, 伊東 隼人, 小田 昌宏, 小宮山 琢真, 古川 和宏, 宮原 良二, 藤城 光弘, 森 雅樹, 高畠 博嗣, 名取 博, 森 健策: マルチスケール特徴抽出による胃壁マイクロCT像からの解剖学的構造セグメンテーション手法, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vol.21, no.4 19(VII)‒2, pp.273-274, 東京大学本郷キャンパス 工学部2号館 (2019/11/23)
  26. 大石 仁美, 伊東 隼人, 森 悠一, 三澤 将史, 林 武雅, 奥村 大志, 小田 昌宏, 工藤 進英, 森 健策: 内視鏡的粘膜下層剝離術中の自動穿孔検出に関する初期的検討, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vol.21, no.4 19(II)‒2, pp.232-233, 東京大学本郷キャンパス 工学部2号館 (2019/11/22)
  27. 魯 仲陽, 伊東 隼人, 小田 昌宏, 林 雄一郎, 渡谷 岳行, 阿部 修, 橋本 正弘, 陣崎 雅弘, 森 健策: Grad‒CAMを用いた脳CT像からのくも膜下出血の出血領域可視化に関する検討, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vo.21, no.4 19(I)‒6, pp.229-230, 東京大学本郷キャンパス 工学部2号館 (2019/11/22)
  28. 日比 裕太, 林 雄一郎, 北坂 孝幸, 伊東 隼人, 小田 昌宏, 三澤 一成, 森 健策: グラフ畳み込みニューラルネットワークによる腹部動脈血管名自動命名におけるデータ拡張による精度改善, 第28回日本コンピュータ外科学会大会 (JSCAS 2019) 2019年11月22日(金)-24日(日), 日本コンピュータ外科学会誌, vol.21, no.4 19(I)-4, pp.226-227, 東京大学本郷キャンパス 工学部2号館 (2019/11/22)
  29. 日比 裕太, 林 雄一郎, 北坂 孝幸, 伊東 隼人, 小田 昌宏, 三澤 一成, 森 健策: グラフ畳み込みニューラルネットワークを用いた腹部動脈血管名自動命名の初期検討, 第38回日本医用画像工学会大会（JAMIT 2019) 2019年7月24日(水)-7月26日(金), 第38回日本医用画像工学会大会予稿集, OP5-11, 奈良春日野国際フォーラム (2019/07/26)
  30. 西尾 光平, 小田 紘久, 千馬 耕亮, 北坂 孝幸, 伊東 隼人, 小田 昌宏, 檜 顕成, 内田 広夫, 森 健策: 小児腸閉塞患者のCT像におけるCycleGANを用いた電子洗浄手法の検討, 第38回日本医用画像工学会大会（JAMIT 2019) 2019年7月24日(水)-7月26日(金), 第38回日本医用画像工学会大会予稿集, OP3-20, 奈良春日野国際フォーラム (2019/07/25)
  31. ヴィラード ベンジャミン, 伊東 隼人, 小田 昌宏, 森 悠一, 一政 克朗, 三澤 将史, 工藤 進英, 森 健策: Polyp size classification in colorectal cancer using a Siamese network, 第38回日本医用画像工学会大会（JAMIT 2019) 2019年7月24日(水)-7月26日(金), 第38回日本医用画像工学会大会予稿集, OP2-14, 奈良春日野国際フォーラム (2019/07/25)
  32. 御手洗 翠, 小田 紘久, 杉野 貴明, 守谷 享泰, 伊東 隼人, 小田 昌宏, 小宮山 琢真, 森 雅樹, 高畠 博嗣, 名取 博, 森 健策: 表現学習とSVMによる胃壁マイクロCT像の半教師ありセグメンテーション手法, 第38回日本医用画像工学会大会（JAMIT 2019) 2019年7月24日(水)-7月26日(金), 第38回日本医用画像工学会大会予稿集, OP2-08, 奈良春日野国際フォーラム (2019/07/25)
  33. 伊東 隼人, 森 悠一, 三澤 将史, 小田 昌宏, 工藤 進英, 森 健策: 深層学習における学習データセット規模拡大に応じた分類精度向上に関する実験的検討 ～超拡大大腸内視鏡画像における腫瘍性病変分類に向けた特徴量抽出～, 第38回日本医用画像工学会大会（JAMIT 2019) 2019年7月24日(水)-7月26日(金), 第38回日本医用画像工学会大会予稿集, OP1-24, 奈良春日野国際フォーラム (2019/07/24)
  34. 小田 紘久, 西尾 光平, 北坂 孝幸, 天野 日出, 千馬 耕亮, 内田 広夫, 鈴木 耕次郞, 伊東 隼人, 小田 昌宏, 森 健策: 少量のラベルデータを用いた学習によるイレウス症例CT像における拡張腸管の自動抽出, 第38回日本医用画像工学会大会（JAMIT2019) 2019年7月24日(水)-7月26日(金), 第38回日本医用画像工学会大会予稿集, OP1-15, 奈良春日野国際フォーラム (2019/07/24)
  35. 伊東 隼人, 森 悠一, 三澤 将史, 小田 昌宏, 工藤 進英, 森 健策: 超拡大内視鏡における病理画像分類のための特徴選択法, 第21回画像の認識・理解シンポジウム (MIRU 2018) 2018年8月5日(水)-8月8日(金), 画像の認識・理解シンポジウム Extended Abstract集, PS2-17, 札幌コンベンションセンター (2018/08/07)
  36. 伊東 隼人, 森 悠一, 三澤 将史, 小田 昌宏, 工藤 進英, 森 健策: 不均衡データセットからの学習データセット構築法 -機械学習に基づく医用画像分類に向けて-, 第27回日本コンピュータ外科学会大会 (JSCAS 2018) 2018年11月9日(金)-11日(日), 日本コンピュータ外科学会誌, vol.20, no.4 18(Ⅲ)-5, pp.261-262, 奈良県文化会館 (2018/11/09)
  37. 三澤 将史, 工藤 進英, 森 悠一, 伊東 隼人, 森 健策: AIを実装した医療機器を世に出すための通ったいばらの道, 第27回日本コンピュータ外科学会大会 (JSCAS 2018) 2018年11月9日(金)-11日(日), 日本コンピュータ外科学会誌, vol.20, no.4 シンポジウム①, pp.220, 奈良県文化会館 (2018/11/09)
  38. 西尾 光平, 小田 紘久, 千馬 耕亮, 北坂 孝幸, Holger R. Roth, 伊東 隼人, 林 雄一郎, 小田 昌宏, 檜 顕成, 内田 広夫, 森 健策: イレウス診断支援システムにおける閉塞部位の誤検出修正及び改善ツールの構築, 第27回日本コンピュータ外科学会大会 (JSCAS 2018) 2018年11月9日(金)-11日(日), 日本コンピュータ外科学会誌, vol.20, no.4 18(Ⅹ)-3, pp.348-349, 奈良県文化会館 (2018/11/11)
  39. 小澤 卓也, 小田 紘久, 伊東 隼人, 北坂 孝幸, Holger R. Roth, 小田 昌宏, 林 雄一郎, 三澤 一成, 伊藤 雅昭, 竹下 修由 , 森 健策: U-Netを用いた腹腔鏡動画像における出血領域検出に関する検討, 第27回日本コンピュータ外科学会大会 (JSCAS 2018) 2018年11月9日(金)-11日(日), 日本コンピュータ外科学会誌, vol.20, no.4 18(6)-10, pp.370, 奈良県文化会館 (2018/11/11)
  40. 森 健策, 伊東 隼人, 三澤 将史, 森 悠一, 工藤 進英: 超拡大内視鏡におけるAI, 日本光学会年次学術講演会（OPJ2018) 2018年10月30(火)-11月2日(金), 日本光学会年次学術講演会講演予稿集, pp.226-227, 筑波大学東京キャンパス 文京校舎 (2018/11/01)
  41. 伊東 隼人, Holger Roth, 三澤将史, 森悠一, 小田昌宏, 工藤進英, 森健策: 教師なし深度推定を利用したRGB-D特徴抽出に基づくポリープのトリナリサイズ推定, 第37回日本医用画像工学会大会（JAMIT 2018) 2018年7月25日(水)-7月27日(金), 第37回日本医用画像工学会大会予稿集, OP14-4, 筑波大学 天王台キャンパス 大学会館 (2018/07/27)
  42. 小澤 卓也, 小田 紘久, 伊東 隼人, 北坂 孝幸, Holger R. Roth, 小田 昌宏, 林 雄一郎, 三澤 一成, 伊藤 雅昭, 竹下 修由, 森 健策: 機械学習による内視鏡動画インスタンスセグメンテーションのための手動アノテーションツールの開発, 第37回日本医用画像工学会大会（JAMIT 2018) 2018年7月25日(水)-7月27日(金), 第37回日本医用画像工学会大会予稿集, OP1-7, 筑波大学 天王台キャンパス 大学会館 (2018/07/25)
  43. 西尾 光平, 小田 紘久, 千馬 耕亮, 北坂 孝幸, Holger Roth, 伊東 隼人, 小田 昌宏, 檜 顕成, 内田 広夫, 森 健策: Fast Marching Algorithmに基づく小児CT像からの腸管閉塞部位検出手法, 第37回日本医用画像工学会大会（JAMIT 2018) 2018年7月25日(水)-7月27日(金), 第37回日本医用画像工学会大会予稿集, OP1-6, 筑波大学 天王台キャンパス 大学会館 (2018/07/25)
  44. 伊東 隼人，森 悠一，三澤将史，小田昌宏，工藤進英，森 健策: 超拡大大腸内視鏡画像を利用した病理自動診断 〜腫瘍性病変に関する分類精度解析〜, 第26回日本コンピュータ外科学会大会 (JSCAS 2017) 2017年10月28日(土)-30日(月), 日本コンピュータ外科学会誌, vol.19, no.4, 17(XII)-3, pp.319-320, 名古屋大学 東山キャンパス 豊田講堂・シンポジオン (2017/10/30)
  45. 伊東 隼人，酒井智弥, 井宮淳: スパース表現に基づく識別手法は非線形クラス部分空間に対して頑健か? ～見えに基づく物体認識における検証～, 第14回画像の認識・理解シンポジウム (MIRU 2011) 2011年7月20日(水)-7月22日(金), 画像の認識・理解シンポジウム論文集, IS1-15, pp.177-184, 金沢文化ホール (2011/7/20)

Technical Report

  1. 小野坂 捺, 伊東 隼人, 小田 昌宏, 三澤 将史, 森 悠一, 工藤 進英, 森 健策: 教師なしモデルベース深度推定を利用した大腸の3次元形状復元, 電子情報通信学会技術研究報告(MI), MI2023-60, vol. 123, no. 411, pp. 87-90, 沖縄県青年会館 (2024/3/3)
  2. 伊東 隼人, 小田 昌宏, 申 忱, 王 成, 三浦 幹太, 佐藤 淳哉, 大竹 義人, 備瀬 竜馬, 古川 亮, 本谷 秀堅, 増谷 佳孝, 森 健策: MICCAI 2022参加報告, 電子情報通信学会技術研究報告(MI), MI2022-79, vol. 122, no. 417, pp. 26-37, 沖縄県青年会館 (2023/3/6)
  3. Hayato Itoh, Masashi Misawa, Yuichi Mori, Shin-Ei Kudo, Masahiro Oda, Kensaku Mori: Analysis of Object Detection Model Towards Precise Colorectal-Polyp Detection, IEICE Technical Report, MI2021-63, vol. 121, no. 347, pp. 76-81, Online (2022/1/26)
  4. 伊東 隼人, 潘 冬平, 小澤 卓也, 小田 昌宏, 竹下 修由, 伊藤 雅昭, 森 健策: 大規模腹腔鏡動画像データベース構築に向けたオンラインアノテーションツールの開発, 電子情報通信学会技術研究報告(MI), MI2021-65, vol. 121, no. 347, pp. 86-87, オンライン開催 (2022/1/26)
  5. 伊東 隼人, 小田 昌宏, 申 忱, 大竹 義人, 花岡 昇平, 諸岡健一, 本谷 秀堅, 古川 亮, 増谷 佳孝, 森 健策: MICCAI 2021参加報告, 電子情報通信学会技術研究報告(MI), MI2021-67, vol. 121, no. 347, pp. 89-99, オンライン開催 (2022/1/26)
  6. 日比 裕太, 林 雄一郎, 北坂 孝幸, 伊東 隼人, 小田 昌宏, 三澤 一成, 森 健策: Spectral-based Convolutional Graph Neural Networksを用いた腹部動脈領域の血管名自動命名に関する研究, 電子情報通信学会技術研究報告(MI), MI2020-89, Vol. 120, no. 431, pp. 176-181, オンライン開催 (2021/3/17)
  7. 御手洗 翠, 小田 紘久, 杉野 貴明, 守谷 享泰, 伊東 隼人, 小田 昌宏, 小宮山 琢真, 古川 和宏, 宮原 良二, 藤城 光弘, 森 雅樹, 高畠 博嗣, 名取 博, 森 健策: ニューラルネットワークとSpherical K-meansを用いた胃壁マイクロCT像からの層構造および腫瘍抽出の検討,電子情報通信学会技術研究報告(MI), MI2020-17, vol. 120, no. 156, MI2020-17, pp. 1-6, オンライン開催 (2020/9/20)
  8. 西尾 光平, 小田 紘久, 千馬 耕亮, 北坂 孝幸, 林 雄一郎, 伊東 隼人, 小田 昌宏, 檜 顕成, 内田 広夫, 森 健策: CycleGANによる腸管電子洗浄とその腸管閉塞部位検出への応用, 電子情報通信学会技術研究報告(MI), MI2019-122, vol. 119, no. 399, pp. 243-248, 沖縄県青年会館 (2020/1/30)
  9. 小田 昌宏, 伊東 隼人, 宮内 翔子, 諸岡 健一, 松崎 博貴, 花岡 昇平, 古川 亮, 増谷 佳孝, 森 健策: MICCAI 2019参加報告, 電子情報通信学会技術研究報告(MI), MI2019-117, vol.119, no.399, pp.219-226, 沖縄県青年会館 (2020/1/30)
  10. 魯 仲陽, 小田 昌宏. 林 雄一郎, 伊東 隼人, 渡谷岳行, 阿部 修, 橋本正弘, 陣崎雅弘, 森 健策: 深層学習によるSMOTEを用いた不均衡クモ膜下出血データの自動検出に関する研究, 電子情報通信学会技術研究報告(MI), MI2019-75, vol. 119, no. 399, pp. 47-52, 沖縄県青年会館 (2020/1/29)
  11. Hayato Itoh, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-Ei Kudo, Kensaku Mori: Analysis and Feature Selection of CNN Features ～Recognition of Neoplasia by using Endocytoscopic Images , IEICE Technical Report, MI2019-48, vol. 119, no. 193, pp. 129-134, Okayama University (2019/9/5)
  12. Hayato Itoh, Yuichi Mori, Masashi Misawa, Masahiro Oda, Shin-Ei Kudo, Kensaku Mori: Feature Selection from Imbalanced Data ～Pathological Pattern Classification in Endocytoscopic Images～, IEICE Technical Report, MI2018-87, vol. 118, no. 412, pp. 109-114, Okinawa-ken Seinen Kaikan (2019/1/23)
  13. 小田 昌宏, 大竹 義人, 伊東 隼人, 杉野 貴明, 斉藤 篤, 古川 亮, 大西 峻, 井宮 淳, 森 健策: MICCAI2018参加報告, 電子情報通信学会技術研究報告(MI), MI2018-111, vol. 118, no. 412, pp. 221-228, 沖縄県青年会館 (2019/1/23)
  14. 舘 高基, 小田 昌宏, 林 雄一郎, 伊東 隼人, 中村 嘉彦, 北坂 孝幸, 三澤 一成, 森 健策: 経時CT像間の腹部臓器の変形を考慮したリンパ節自動対応付け手法の検討, 電子情報通信学会技術研究報告(MI), MI2018-84, vol. 118, no. 412, pp. 97-102, 沖縄県青年会館 (2019/1/22)
  15. Hayato Itoh, Yuichi Mori, Misawa Masashi, Masahiro Oda, Shin-Ei Kudo, Kensaku Mori: Feature-selection method based on Grassmann distance for the classification of neoplastic polyps on endocytoscopic images,IEICE Technical Report, MI2017-81, Vol. 117, No. 518, pp. 51-56, Ishigaki Island Hotel Miyahira (2018/3/19)
  16. 伊東 隼人, 森 悠一, 三澤 将史, 小田 昌宏, 工藤 進英, 森 健策: 畳み込みニューラルネットワークを利用した超拡大大腸内視鏡画像における腫瘍・非腫瘍の分類, 電子情報通信学会技術研究報告(MI), MI2017-44, vol. 117, no. 220, pp. 17-21, 千葉大学 西千葉キャンパス (2017/9/25)
  17. Kaori Tanji, Hayato Itoh, Atsushi Imiya, Naohiro Manago, Hiroaki Kuze: Statistical Properties of Hyperspectral Images, IEICE Technical Report, PRMU2017-16, vol. 117, no. 49, pp. 81-85, Nagoya Institute of Technology (2017/5/26)
  18. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Deep Subspace Methods - Pattern Recognition using Hierarchical Structure of Linear Subspaces, IEICE Technical Report, PRMU2017-18, vol. 117, no. 49, pp. 93-98, Nagoya Institute of Technology (2017/5/26)
  19. Kaori Tanji, Atsushi Imiya, Hayato Itoh: Statistical properties of Colour HoG, IEICE Technical Report, PRMU2016-147, vol. 116, no. 411, pp. 327-332, Kyoto University Yoshida Campus (2017/1/20)
  20. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Object Oriented Data Analysis for Volumetric Medical Data using Multiway Principal Component Analysis, IEICE Technical Report(MI), MI2016-57 vol. 116, no.225, pp.41-46, Tokyo University of Agriculture and Technology Koganei Campus (2016/9/16)
  21. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Tensor-Based Methods for Dimension Reduction of Volumetric Data, IEICE Technical Report, PRMU2015-197, vol. 115, no. 517, pp.197-202, AIST Tokyo Waterfront (2016/3/25)
  22. Atsushi Imiya, Hayato Itoh: Eigenfunctions in Linear Scale Space, IEICE Technical Report, PRMU2015-107, vol. 115, no. 388, pp. 87-92, Shinshu University (2015/12/22)
  23. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Mathematical Properties of the Gradient-Based Discriminative Methods, IEICE Technical Report, PRMU2015-50, vol. 115, no. 98, pp.107-111, Niigata University Tokimate (2015/6/19)
  24. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Second-Order Tensor Principal Component Analysis Meets Two-Dimensional Singular Value Decomposition, IEICE Technical Report, PRMU2015-14, vol. 115, no. 24, pp.71-74, Mie University (2015/5/15)
  25. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: 3D Global Image Registration Using Local Linear Property in Sparse Dictionary, IEICE Technical Report, PRMU2013-102, vol. 113, no. 402, pp.125-130, Osaka University Toyonaka Campus (2014/1/23)
  26. Hayato Itoh, Atsushi Imiya, Tomoya Sakai: Explicit Local Linear Method for 2D Affine Image Registration, IEICE Technical Report, PRMU2013-82, vol. 113, no. 346, pp. 85-90, Mie University (2013/12/13)
  27. Hayato Itoh, Tomoya Sakai, Atsushi Imiya: Validation of Dimension Reduction Methods for Two-Dimensional Image Pattern Classification, IEICE Technical Report, PRMU2012-183, vol. 112, no. 495, pp. 19-24, University of Electro-Communications (2013/3/14)
  28. Hayato Itoh, Tomoya Sakai, Atsushi Imiya: Effects of Dimension Reduction on Appearance-Based Pattern Classification, IEICE Technical Report, PRMU2012-74, vol. 112, no. 357, pp. 25-30, Yamagata University Yonezawa Campus (2012/12/6)
  29. Hayato Itoh, Tomoya Sakai, Atsushi Imiya: NN-Based Local Subspace Method for Image Registration with Sparse Dictionary, IEICE Technical Report, PRMU2012-48, vol. 112, no. 197, pp. 179-184, Tokyo University of Agriculture and Technology Koganei Campus (2012/9/3)
  30. Hayato Itoh, Shuang Lu, Tomoya Sakai, Atsushi Imiya: Efficient Global Image Registration Using Local Linearity of Transformed Image, IEICE Technical Report, MI2011-68, vol. 111, no, 331, pp. 31-36, University of Hyogo Port Island Campus (2011/11/29)
  31. Shuang Lu, Hayato Itoh, Tomoya Sakai, Atsushi Imiya: Global Image Registration using Random Projection, Information Processing Society of Japan Technical Report, Vol. 2011-CVIM-177, No.7, pp. 1-7, Osaka University Suita Campus (2011/5/19)
  32. Hayato Itoh, Tomoya Sakai, Atsushi Imiya: Pattern Classification by Sparse Subspace Method, Information Processing Society of Japan Technical Report, Vol. 2010-CVIM-172, No.33, pp. 1-7, Nagoya Institute of Technology (2010/5/27)

Invited Talk

  1. 伊東 隼人: 古くて新しい画像パターン認識, 第2回 JAMIT若手医用画像工学シンポジウム: SAMIT2024 ポストワークショップ, 福岡大学 (2024/9/22)
  2. 伊東 隼人: 計算機⽀援診断のための画像パターン解析, 第62回日本生体医工学会大会 オーガナイズドセッション, 名古屋国際会議場 (2023/5/20)
  3. 伊東 隼人: 画像パターン解析のためのテンソル表現, 医用画像研究会, 名古屋国際会議場 (2023/5/18)
  4. 伊東 隼人: 画像パターン認識とその応用 ―医工学という境界分野に飛び込んで―, 生体医工学シンポジウム2022, オンライン開催 (2022/9/10)
  5. 伊東 隼人: コロナ禍における数理工学研究とその応用, 第1回名古屋大学イニシアティブウェビナー「生命と人工知能」, オンライン開催 (2021/07/29)

Book

  1. 森 健策, 伊東 隼人, ``医療AIとディープラーニングシリーズ 内視鏡画像AI,'' 藤田 広志 (シリーズ監修), 森 健策 (編), 工藤 進英 (編), 森 悠一 (編), 三澤 将史 (編), オーム社, 基礎編 Chapter 1: 概論, pp. 1-23, ISBN978-4-274-22564-2 (2022年11月5日）
  2. 伊東 隼人, ``医療AIとディープラーニングシリーズ 内視鏡画像AI ,''藤田 広志（シリーズ監修）, 藤田 広志 (シリーズ監修), 森 健策 (編), 工藤 進英 (編), 森 悠一 (編), 三澤 将史 (編), オーム社, 事例編 Chapter 14: ポリープ検出 (超拡大内視鏡), pp. 135-144, ISBN978-4-274-22564-2 (2022年11月5日）
  3. 小田 昌宏, 伊東 隼人, ``医療AIとディープラーニングシリーズ 内視鏡画像AI,'' 藤田 広志 (シリーズ監修), 森 健策 (編), 工藤 進英 (編), 森 悠一 (編), 三澤 将史 (編), オーム社, 実践編 Chapter 19: AIによる内視鏡画像分類, pp. 179-198, ISBN978-4-274-22564-2 (2022年11月5日）
Experiences

Career

  • Nov. 2023 - Present, Visiting Scholar, Graduate School of Informatics, Nagoya University
  • Sep. 2023 - Present, Assistant Professor (tenured), Department of Applied Mathematics, Faculty of Science, Fukuoka University
  • Nov. 2020 - Aug. 2023, Designated Assistant Professor, Department of Intelligent Systems, Graduate School of Informatics, Nagoya University
  • Apr. 2017 - Nov. 2020, Research Fellow, Department of Intelligent Systems, Graduate School of Informatics, Nagoya University
  • Apr. 2013 - Mar. 2017, Special Collaboration with Research Students (特別共同利用研究員), Digital Content and Media Sciences Research Division, National Institute of Infomatics
  • Apr. 2010 - Mar. 2011, Special Collaboration with Research Students (特別共同利用研究員), Digital Content and Media Sciences Research Division, National Institute of Infomatics
  • May. 2009 - Mar. 2010, 研究研修生, Digital Content and Media Sciences Research Division, National Institute of Infomatics

Technical Support Stuff

  • Sep. 2013 - 2017, Technical supporter for users in the Institute of Media and Information Technology, Chiba University
  • Apr. 2010 - Feb. 2013, Technical supporter for users in the Institute of Media and Information Technology, Chiba University

Research Assistant

  • Sep. 2015 - Feb. 2016, Chiba University
  • Sep. 2014 - Feb. 2015, Chiba University
  • Sep. 2013 - Feb. 2014, Chiba University
  • Sep. 2012 - Feb. 2013, Chiba University

Teaching Assistant

  • 2011-2017, Teaching Assistant in classes for undergraduate and master course students, Chiba University

Tutorial for Undergraduate Students

  • 2010-2015, Tutor for students at the 1st year of their master course in s in Imiya and Kawamoto Lab, Chiba Univeristy. In the tutorial, the following topics are included.
    • How to use Linux in laboratory life (terminal, bash, LaTeX, Gnuplot, Octave)
    • Introduction to C++ coding as the super set of C (with OpenCV and Boost)
    • Basics of numerical computation (gradient method, Newton method, least-square method, conjugate gradient method, linear programming)
    • Basics of Computer Vision (discrete representation of image, geometrical transform and interpolation, projective geometry, epipolar geometry, homography estimation, camera calibration, detection of local features, search for corresponding points, robust estimation, 3D reconstruction)
    This tutorial was supported by Prof. Akihiro Sugimoto (NII).

Lecture

  • 2024年度～, プログラミングⅠおよび実習
  • 2023年度～, 多変量解析
  • 2023年度～, アルゴリズムとデータ構造

Association

  • IEICE (The Institute of Electronics, Information and Communication Engineers), member
  • JAMIT (The Japanese Society of Medical Imaging Technology), member & director
  • JAMIT Young Committee (JAMIT若手委員会), chair
  • JSCAS (The Japan Society of Computer Aided Surgery), member
  • JSNMSciEng (日本核医学会 核医学理工分科会), member

Referee

  • Conference: MICCAI, MIDL, ICPR, IPCAI, IJCAI, MIRU
  • IEEE Trans. Image Processing (TIP)
  • IEEE Trans. Medical Imaging (TMI)
  • Medical Image Analysis (MedIA)
  • Neurocomputing
  • Machine Vision and Applications
  • International Journal of Computer Assisted Radiology and Surgery (IJCARS)
  • SPIE Journal of Medical Imaging (JMI)
  • IEICE Trans. Infromation and Systems
  • IEICE Trans. Fundamentals of Electronics Communications and Computer Sciences
  • JAMIT Medical Image Technology
  • ...for the more details, please refere to my WOS page (records of peer reviews)

Contribution to Conferences and Workshops

  • 2024, Chair, The second Symposium on Advanced Medical Imaging Technology for Young Investigators (SAMIT 2024)
  • 2023, PC member, The first Symposium on Advanced Medical Imaging Technology for Young Investigators (SAMIT 2023)
  • 2022, Local organiser, The 41st Annual Meeting of the Japanese Society of Medical Imaging Technology (JAMIT 2022)
  • 2022, MIRU Senior Evaluator
  • 2020, PC member, The 29th International Joint Conference on Artificial Intelligence and the 17th Pacific Rim International Conference on Artificial Intelligence (IJCAI-PRICAI2020)
  • 2017, Local organiser, The 26th Annual congress of Japan Society of Computer Aided Surgery (JSCAS 2017)
  • 2016, System administrator, Workshop on Mathematical and Computational Methods in Biomedical Imaging and Image Analysis (ACCV-2017 workshop)
  • 2015, System administrator, Workshop on Mathematical and Computational Methods in Biomedical Imaging and Image Analysis (PSIVT-2016 workshop)
  • 2013, System administrator, Workshop on Computer Vision in Vehicle Technology:From Earth to Mars (ICCV2013 workshop)
  • 2012, Support stuff, International Conference on Pattern Recognition (ICPR 2012)
  • 2012. Local organiser, Joint IAPR International Workshops on Structural and Syntactic Pattern Recognition (SSPR 2012) and Statistical Techniques in Pattern Recognition (SPR 2012)
  • 2012, System administrator & support stuff, Joint IAPR International Workshops on Structural and Syntactic Pattern Recognition (SSPR 2012) and Statistical Techniques in Pattern Recognition (SPR 2012)
  • 2012, System administrator, Workshop on Computer Vision in Vehicle Technology:From Earth to Mars (ECCV-2012 workshop)
  • 2011, System administrator, Workshop on Computer Vision in Vehicle Technology:From Earth to Mars (ICCV-2011 workshop)

Visit

Others

Award

  • 2018年, 日本医用画像工学会 奨励賞
  • 2018年, 日本コンピュータ外科学会 講演論文賞
  • 2018年, 電子情報通信学会 医用画像研究会 MI研究奨励賞
  • 2010-2012年, 日本学生支援機構第一種奨学金, 特に優れた業績による返還免除

Grant

  • 2024年-2026年, 伊東 隼人 (研究代表者), 令和6年度 福岡大学 若手・女性研究基盤構築支援事業, 機械学習モデルの内部表現に関する研究
  • 2023年-2026年, 伊東 隼人 (研究代表者), 科学研究費補助金 若手研究, 対象依存型データ解析に基づく頑健な3次元画像パターン認識
  • 2014年, 伊東 隼人, 融合科学研究科 AGSTプログラム採択
  • 2013年, 伊東 隼人, 融合科学研究科 大学院生海外派遣プログラム採択
  • 2012年, 伊東 隼人, 融合科学研究科 大学院生海外派遣プログラム採択